Extension

By Krista Floer

Here are the instructions: Extend the sides of the triangle and let Barney begin his journey from a point outside the triangle. His path is slightly redefined -- rather than "bouncing" when he comes to a wall, he crosses the wall to change direction and continues to travel a path parallel to a side of the triangle. Construct a GSP image and explore.

While exploring, I wanted to know about the length of Barney's path. Was it constant? Was a ratio involved? Could there be a formula? After thinking for a minute, I deduced that a constant path length could not be possible. That just did not make sense. I did not think that a ratio was involved, so I went about trying to find a formula for the path length. I came up with this proof that derives a formula.

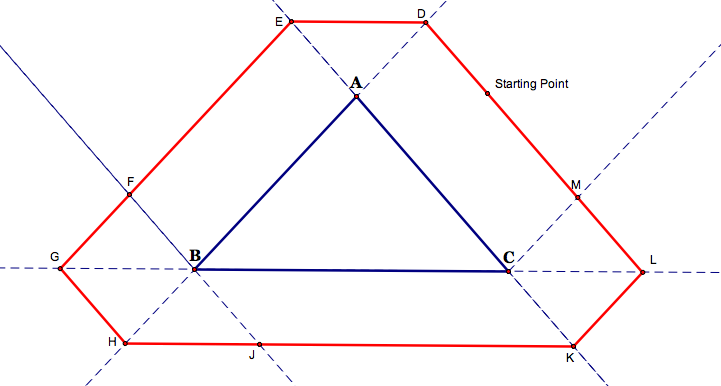
First, consider this picture of a sample path for Barney:

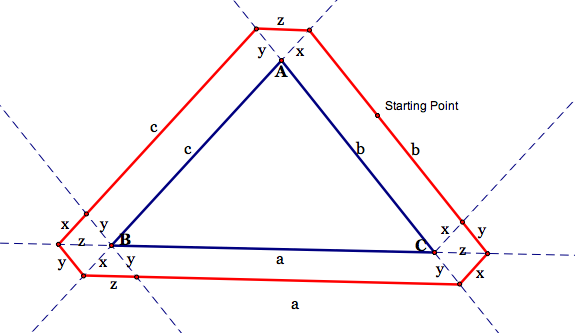
Like all of the other proofs for this problem, parallelograms are found everywhere. I will leave the exact proof for the reader, but I have labelled all of the corresponding sides ONLY by using parallelograms.

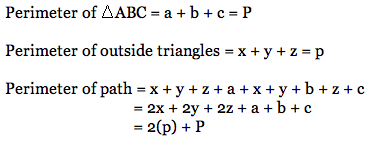So we can see the length of the path that Barney takes when his starting point is outside the triangle is equal to 2 times the perimeter of the small inner triangle plus the perimeter of triangle ABC.