

A centroid of a triangle is the point where the three medians of the triangle meet. A median of a triangle is a line segment from one vertex to the mid point on the opposite side of the triangle.
The centroid is also called the center of gravity of the triangle. If you have a triangle plate, try to balance the plate on your finger. Once you have found the point where it will balance, that is the centroid of that triangle.
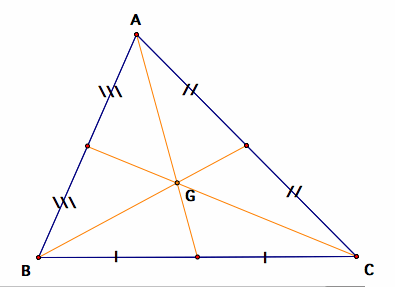
The centroid of triangle ABC
Now, someone might raise the question of how do we know if the three medians actually meet at one point. That is a very good question and lets test a couple of different triangles to see if this is the case. Click HERE to open a GSP file and experiment yourself.
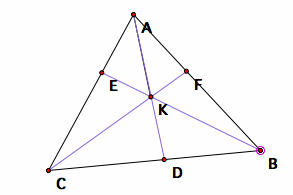
To test whether the three medians were concurrent, let us first construct the midpoints D, E, and F on each sides of the triangle. Then, let us connect the points B and E, and C and F and label the intersection point G.
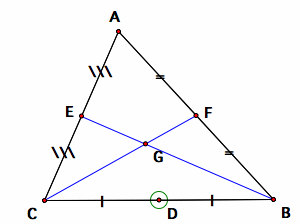
Then, let us construct a ray from point A to point G, and test if this ray (orange colored) goes through the mid point D for different shape of triangles.
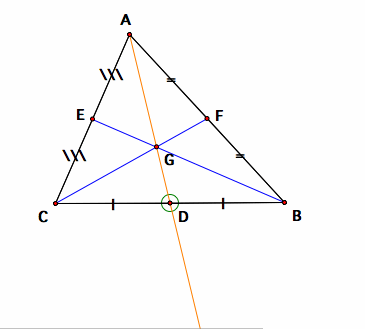
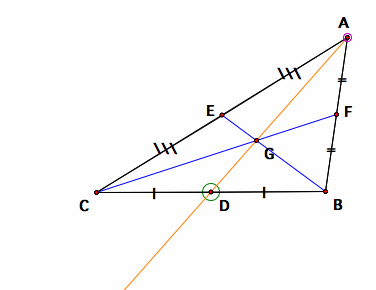
Testing of whether three medians intersect at one point
From these samples, it is clear that the ray AG arrows through the mid point D exactly, and the three medians indeed meet at one point. To prove the concurrency of the three medians, we will need to use the Ceva's theorem.
This theorem was proved by Giovanni Ceva (1648-1734). To get a full introduction to this theorem, CLICK HERE, and to see a proof of Ceva's theorem, CLICK HERE.
Theorem: In a triangle ABC, three lines AD, BE and CF intersect at a single point K if and only if
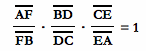
Now using Ceva's theorem, it will be straightforward to prove that the three medians intersect at one point. Since the medians divide each sides of the triangle in half, it follows that AF = FB = 1/2, BD = DC = 1/2, and CE = EA = 1/2. Hence, AF/FB = 1, BD/DC = 1, CE/EA = 1, and the product of the three ratios equal to 1.
There is another special characteristic of the centroid. Can you see any patterns from the diagrams below?
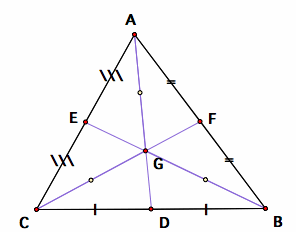
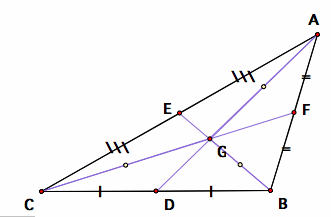
Do you see anything special about the Centroid?
The centroid divides each median in a special ratio 2:1. In the diagrams above, I inserted the mid points of AG, BG and CG, to make it easier to compare the lengths. Now let us prove that the centroid divides each median in the ratio 2:1.
The centroid divides each median in the ratio 2:1.
![]()

Proof:
Let us connect the two midpoints E and F,
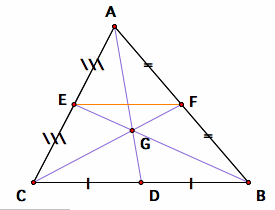
Then the triangles AEF and ACB are similar, because
It follows that because triangles AEF and ACB are similar, the lines EF and CB are parallel and CB = 2 * EF.
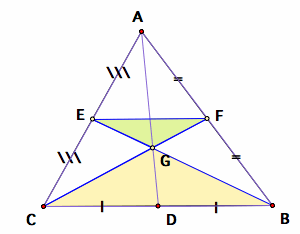
Now look at triangles EGF and BGC. Because the lines EF and CB are parallel,
![]()
Also, angle GDE equals angle GBC because they are opposite one another.
Thus, triangles EGF and BGC are similar. Furthermore, because CB = 2 * EF, this means that the length of the sides of the triangles BGC and EGF are in the ratio 2:1, and we have
![]()
Similary, by constructing a line from point D to F, and using the two similar triangles DFG and AGC, we can prove that
![]()