

Assignment 3: Explorations of Quadratics
By: Mary Wisniewsky
Let's explore the quadratic equation
![]()
also the various forms of this equation when its set equal to zero.
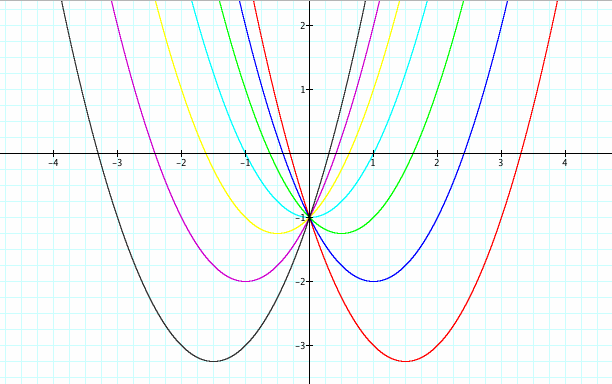
First let's take a look at the equation when a=c=1 are fixed values and b is varied.
The roots or factors of the equation are the value(s) of x when the curve intersects the x-axis. Some quadratic equations can yield 2 real roots, 1 real root, or two complex roots.
What kind of roots do we get when b is varied and a=c=1?
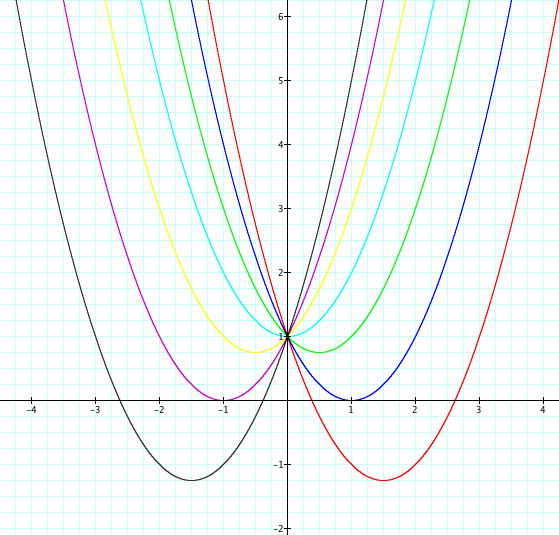
As you can see from the above graph, When b=-3 & b=3, the equation has two real roots.
When b=-2 & b= 2, the equation has one real root at x=1 and x=-1 respectively. When a quadratic equation contains one real root, the curve is going to lie tangent to the x-axis.
When b=-1,0,& 1, the curve does not intersect the x-axis. Therefore the equation contains complex roots.
Notice how all of the curves intersect at one point (0,1):
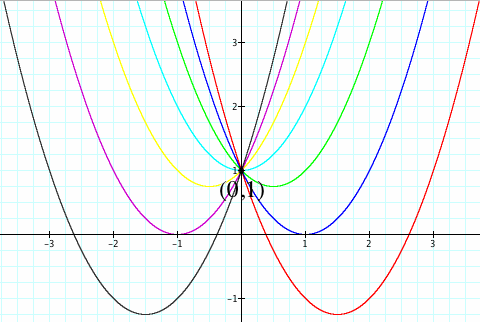
This shows us the y-intercept for all of these quadratic equations.
How can we find the vertex for each curve?
If we get the quadratic equation in the form as it is in assignment 2, then from our discovery in assignment 2 we can find the vertex of the curve.
Start by completing the square for the original equation when a=c=1.
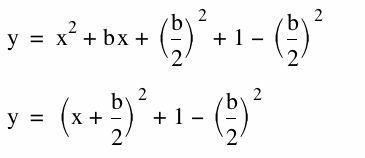
So now that we have in it in the proper form from assignment 2, we can find our vertex.
So let's take a look at the vertex when b=2. From our graph, it looks like the vertex is supposed to be the root (-1,0). For (d,f), we have:
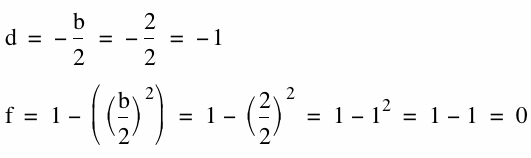
(d,f)=(-1,0) which according to our graph is the vertex.
When you change b to n for the "d,f" form of the quadratic equation, and show it overlaying the original graphs, you can see how this curves intersect all of the vertices of the curves. Check it out on this video.
Now with all the information we have seen thus far, let's take a look at the original equation when a=c=1 in the xb plane (b=y).
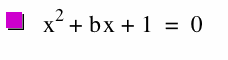
Notice how there is gap in the graph when the curve in between -2 < b < 2. Do you remember the results we found for the roots when -2 < b < 2?
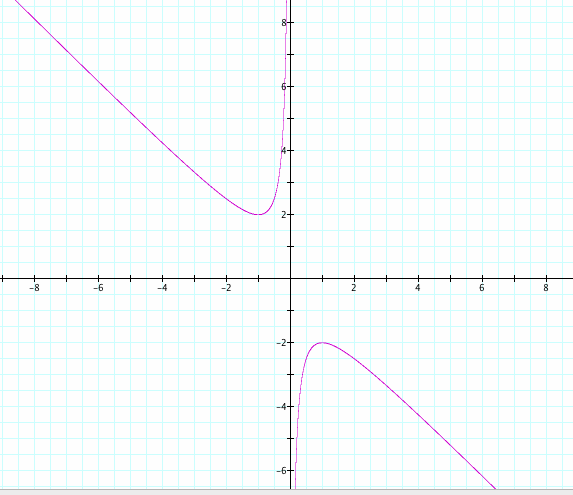
Take a look at the below graph which also includes b=3, b=2, b=1, b= -2, b=-4

The lines b=3 and b=4 intersect the curve twice. When b=3 in the first graph shown, we discovered that for that case the equation contained two real roots.
Now observe the lines b=2, b=-2. These lines lie tangent to the curves and intersect at one point respectively. Similarly, we found for these cases for b values, that the quadratic equation contained one real root and lied tangent to the y-axis.
Finally let's answer our question about the big gap. Take a look at when b=1. This line does not intersect the curves. Also from our original graph of when -2 < b < 2, we found that the quadratic equation contained complex roots and the curves did not intersect the y-axis.
Therefore, we have discovered the relationship between the equation on the xb plane and finding roots.
Let's take a look at different values of c to find what kind of roots the equation would contain.
The below graph contains the quadratic equation when b is varied and when a=1 and c changes to c=-1. (in red)
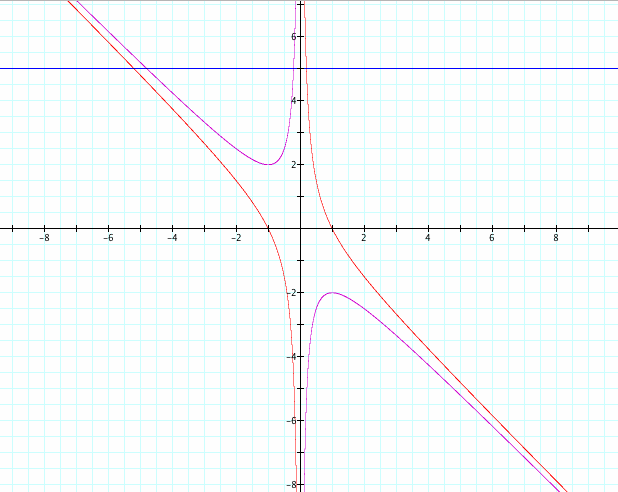
For this case, there is no big gap and the curves intersect twice for all values of b.
From the relationship we just discovered, we can say that for this quadratic equation will always have 2 real roots for all values of b.
Take a look at the graph of this quadratic equation for many values of b and for every quadratic curve there are two real roots.
We have now observed when c=1 and when c=-1. When c=1, for different values of b, there was a combination of real roots and complex roots. In contrast, when c=-1, various values of b all contained real roots.
Take a look at this video when n is varied such that -5 ≤ n ≤ 5.
(Notice how most of the positive integer n values have complex roots as well as real roots. What happens when n=0?
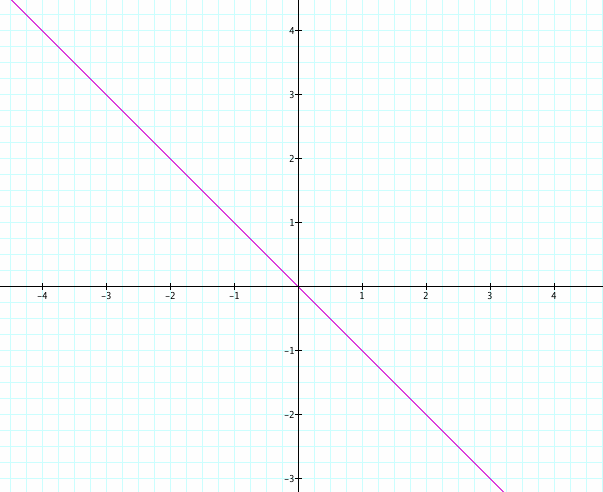
For this case, the curve intersects b values exactly once. Therefore for each value of b, there will be one real root for the quadratic equation.
Continue exploring different values of c with this graphing calculator application!