

Area of Overlapping Circles
by
Ángel M. Carreras Jusino
The purpose of this essay is to explore the area formed by the intersection of overlapping circles and how it is affected by the distance between their centers.
Lets begin with two circles with the same radius, r, overlapping each other (see figure below) and we want to find what is the area of the overlapped section (i.e., green area).
In the following applet can be explored how the distance (d) between the centers of the circles affects the size of the intersection area.
Some observations:
- when d = 0 the area of the intersection is πr2
- when d ≥ 2r the area of intersection is 0
Now, how can we measure the overlapping area?
Note that this area is formed by two overlapping sectors.
So, the plan is to work with one of the circles in finding the area of its sector, then find the area of the segment of the sector by subtracting the area of its triangle, and finally multiply this area by two to get the overlapping area that we want.
(Note: For the purpose of the essay is assumed that the values of d [the distance between the centers of the circles] and r [the radii of the circles] are known.)
Area of the circle's sector
The area of a circle's sector is given by
, where θ is the central angle of the sector in radians.
How can we find the measure of θ ?
Lets look at the following figure.
We have an isosceles triangle with vertices A (center of one of the circles), E, and D (points of intersection of the circles). Note that the height of this triangle is half the distance between the centers of the circles.
Now, to find the measure of the central angle of the sector (or vertex angle of the isosceles triangle) lets divide the isosceles triangle into two right triangles with height d/2, hypotenuse r, and angle formed by the height and hypotenuse of θ/2.
Using trigonometry we have that,
.
Solving for θ we get,
Note that for this equation be defined we need that
, condition that we said earlier that was necessary for the circles to overlap.
Now we can calculate the area of the circle's sector, which is given by
Area of the sector's segment
In order to find the area of the sector's segment we need first to find the area of the triangle that forms it (i.e., triangle ADE.)
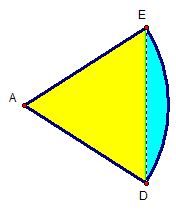
Lets refer back to a figure that we used earlier.
The area of a triangle can be calculated using the formula
, in our case b is DE and h is d/2.
Two approaches to find the area of the triangle
Approach 1. Using the Pythagorean theorem in one of the right triangles to find an expression for the base of the triangle in terms of r and d.
Lets call b the base of the triangle ADE, so the base of the right triangles shown above is b/2.
By the Pythagorean theorem we have,
So the area of the triangle is going to be given by:
Approach 2. Using trigonometry in one of our right triangles and the fact that we already know θ .find an expression for the area in terms of r and θ.
First we define the base and the height of the triangle in terms of r and θ.
and
So the area of the triangle is going to be given by:
.
Now using the double-angle forlmula,
, the area formula can be simplified to
.
Since we now know the area of the triangle, the area of the segment can be determined by the difference in area between the sector and the triangle.
Area of the sector's segment in terms of r and θ
Area of the sector's segment in terms of r and d
Measure of the Overlapping Area
Now that we have the area of the sector segment to find the area of the overlapped section of the circles we only need to multiply it by two.
Therefore, the total area of the overlapped section of two circles with the same radius (r) is given by
with 0 ≤ θ ≤ 2π, where θ is the angle formed by the center of one of the circles (the vertex) and the points of intersection of the circles.
The following graph shows the relation between θ and A,
, when r = 1. Note that the maximun area is obtained when the angle is π (i.e. when the circles completely overlap each other.)
Similarly, the total area of the overlapped section of two circles with the same radius (r) can also be expressed by
with 0 ≤ d ≤ 2r, where d is the distance between the centers of the circles.
The following graph shows the relation between d and A,
, when r = 1. Note that the maximum area is obtained when d = 0 (i.e. when the distance between the centers is zero.)