

Assignment 10:
Investigating Parametric Equations and Magnitude of Line Segments
by
Ángel M. Carreras Jusino
Goals:
1. Write parametric equations of a line segment through (7, 5) with slope of 3.
2. Graph the line segment using your equations.
3. As a line segment, it will have end points. Explore how you would chose endpoints of such that the two distances from (7, 5) are 2 units and 3 units.
Write parametric equations of a line segment through (7, 5) with slope of 3.
There are various ways to write parametric equations of a line segment given a point in it and its slope. One way is to use the coordinates of the point given as the constant terms in the parametric equations. In the case that we are exploring 7 would be the constant for x(t) and 5 the constant for y(t). Now, with the given slope we know how x(t) varies with respect to y(t). For a slope of 3, for each unit that x coordinate travels the y coordinate travels 3 units, this values serve as coefficients of the linear term of the parametric equations. So the parametric equations for the case given is given by

Note that these parametric equations initial point (t = 0) is the point given (7, 5).
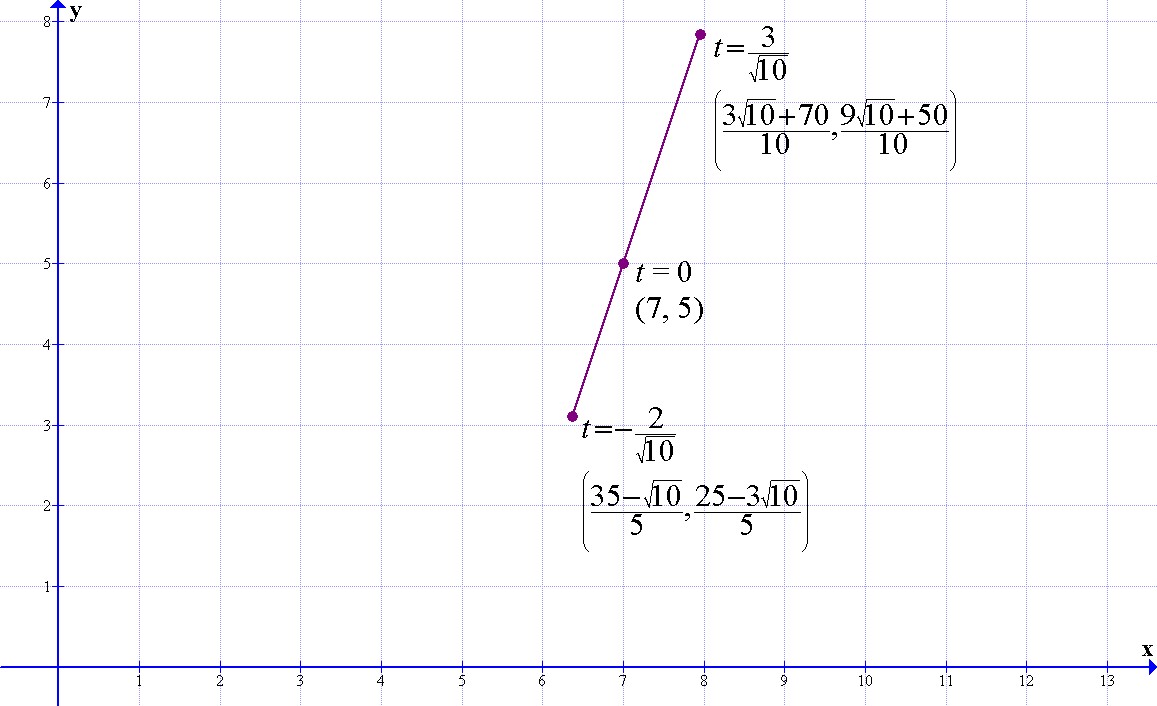
Graph the line segment using your equation.

Explore how you would chose endpoints of the line segment that the distance to the endpoints from (7, 5) are 2 units and 3 units.
We want to find the value of t such that the distance from (x(t), y(t)) to (7, 5) is the one required.
Let r be the distance required, using the distance formula we have
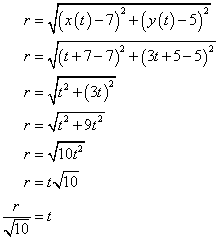
For the first endpoint we want it to be 2 units from (7, 5), therefore using the formula above with r = 2 we get the t value
![]()
Now, using this value in the parametric equations would give us an endpoint in the segment line 2 units from (7, 5), but also using the additive inverse of this value of t would give us an endpoint at the same distance from (7, 5) but in the opposite direction. For this case we will use the additive inverse of t and for the next case (r = 3) we will use the value that the formula provide.
Replacing the value of t found in the parametric equations we get


For the other endpoint we want it to be 3 units from (7, 5), therefore using again the formula with r = 3 we get the t value
![]()
Replacing the value of t found in the parametric equations we get

In this case, if we want to create a segment that lies on the line described by the given parametric equations with a particular length r, we have to chose a and b values such that |a - b| = r, then using the values
![]()
in the parametric equations will get us a segment with the desired length.
This can be generalized for any given parametric equations of a line segment in the following way:
- Let v be the magnitude of of the segment defined by t = 0 and t = 1 (or any two values of t that are which their difference is 1).
- Let r be the desired length of the segment.
- Chose a and b values such that |a - b| = r.
- Using the values of

in the given parametric equations will get us the segment with the desired length.