
EMAT 6680 Assignment 12
Last modified on September 10, 2012.
The Spreadsheet in Mathematics Explorations
The spreadsheet is a utility tool that can be adapted to many different explorations, presentations, and simulations in mathematics. There are spreadsheets available on almost any platform. An essential feature should be the ability to make graphs and charts from the matrix of data. Try using a spreadsheet, such as EXCEL or ClarisWorks, for some of the following investigations.
1. Construct a graph of any function y = f(x) by generating a table of values with the x values in one column and the y values in another.
2. The spreadsheet can be used to display the graph of parametric equations. One way is to place an initial value of the parameter t in cell A1 and increment t in the A column. Put the formula for the x-coordinate, in B1 and the y-coordinate in C1. Fill down to get the appropriate range of t and then graph. Construct some graphs of parametric equations using problems from Assignment 10.
3. Use the spreadsheet to graph equations in polar form. Try some of the examples from Assignment 11.
4. Generate a Fibonnaci sequence in the first column using f(0) = 1, f(1) = 1,
f(n) =
f(n-1) + f(n-2)
.
a.
Construct the ratio of each pair of adjacent terms in the Fibonnaci sequence.
What happens as n increases? What about the ratio of every second term? etc.
b. Explore sequences where f(0) and f(1) are some arbitrary integers other than
1. If f(0)=1 and f(1) = 3, then your sequence is a Lucas Sequence. All such
sequences, however, have the same limit of the ratio of successive terms.
5. Explore problems of growth, e.g. savings, interest compounded.
6. Explore problems of maximization such as the lidless box formed from a 5x8 sheet with a square removed from each corner.
7. Problem: Place four numbers in the first row as follows
A B C D
For each successive row replace the entries by the absolute value of the difference of the entry just above and the entry just to the right in the previous row. In the fourth position use the absolute value of the difference of the fourth and the first (i.e. cycle)
|A-B|
|B-C| |C-D| |D-A|
Will
the process lead to a 0 in all 4 entries for some row?
What is the largest number of rows before a zero row is generated?
(If your answer is less than 10, you should try again)
8. Use the following exploration to generate a function to predict observed data.
a.Take
a cup of hot water and measure its initial temperature (time = 0) and then
record temperature readings each minute for 30 minutes. Make note of the room
temperature . . .
b. Enter the data on a spread sheet and construct a function that will model
the data.
c. Using the function predict the temperature after 45 minutes, 60 minutes, or
300 minutes.
d. Calculate a measure of the error between your model and the observed data by
taking the square of the difference for each time, sum the squares, and divide
by the number of data points. You can use this statistic to guide refinement of
your function to model the data.
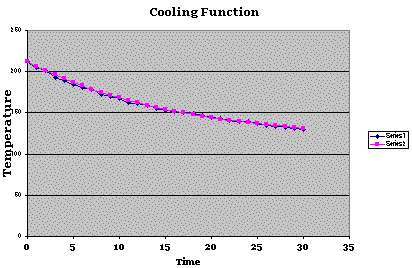
The following spreadsheet graph is from one set of "cooled data." The raw data is plotted in Series 1 (the black squares and line, nearly hidden). The theoretical curve is in Series 2 (the purple).
9. Similar to Problem 8 but use the String data, the length of a guitar string to each fret. . .
That is, the set of data is formed by measuring the length of a guitar string from a fret to the bridge of the guitar. The open string can be thought of as "fret 0", and the length of the open string is the initial measurement. Then make measures for frets 1, 2, . . ., 22 and plot a graph of the points where the fret number is the x coordinate and the length is the y coordinate. To see a completed graph click here. Write a function that produces this graph. Hints, if wanted.
10. Similar to Problem 8 but use the coiled spring data.
This data set has been obtained using a sensor (e.g. a CBL probe) to measure distance and the data was recorded directly into a computer. A "slinky" was held above the probe that had been placed on the floor. When the lower end of the slinky was released it bobbed up and down and the probe measured the distance from the floor 295 times in about 30 seconds.
Excel file for Spring Data
11. Similar to Problem 8 but use the tree data.
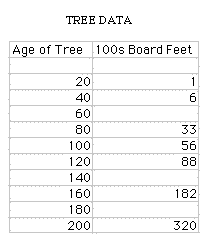
This data is from the lumber industry, giving the approximate number of board feet of lumber per tree in a forest of a given age. What function will fit the data? Predict the harvest for ages other than those given.
Excel file for Tree Data
12. Similar to Problem 8 but use the Stamps data.
This data set is based on the first class letter postage for the US Mail from 1933 to 2008. Plot the data and develop a prediction function. When will the cost of a first class postage stamp reach $1.00? when will the cost be 64 cents? how soon should we expect the next 3 cent increase?
Excel file for Stamps Data
Return to EMAT 6680 Home Page.