Assignment #1

For EMAT 6680
Authored By

Kevin Adams

Exercise 5

Amplitude, Period, and Phase Shift

As Applied to y = a sin(bx+c)

INTRODUCTION:

In this exercise it is important for the student to gain a general understanding of the sin graph. In assisting this understanding, Graphing Calculator can be used to illustrate the ideas that are being learned.

For the purpose of this exercise we will study the equation y=a sin(bx+c). In particular, we want to pay close attention to the effects that changing a, b, and c will have on the graph.

In the description below I will explain how I feel that using Graphing Calculator can help the students learn about this particular graph. Keep in mind that many other graphs could be studied in this same manner. As a matter of fact, it is encouraged that the students be given the opportunity to study the graphs of other functions and develop their on conjectures based on what they discover.

Remember, this is only a guide to a single method that will help the teacher teach and the student learn.

In each of the graphs below, the two variables that are not changing are each set to 1 unless otherwise stated.

Exploring "a":

First, we will explore the effect that different values of "a" has on the graph. I would suggest graphing two or three different graphs for starters. Perhaps you can graph the equations for a=1, a=2, and a=3. From there, ask the students to predict what the graph will look like if a=5, a=50, and a=(-3). The included graphs below will help the students visualize what is happening. While exploring "a" the students should see that the amplitude is changing as "a" changes.

This is a picture of what will happen as the value of "a" changes. The graphs of each line are given below.

y= 3 sin(bx+c)

y= 2 sin(bx+c)

y=1 sin(bx+c)

y= (-1) sin(bx+c)

y= (-2) sin(bx+c)

y= (-3) sin(bx+c)

 

Click Here To See What Happens as "a" Changes From -20 to 20

Exploring "b":

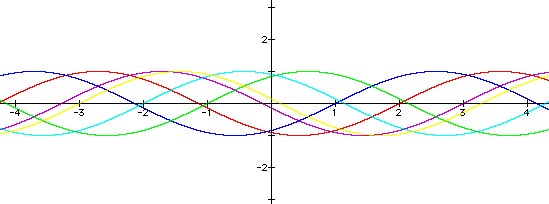
Now we will explore the effect that different values of "b" has on the graph. Once again, start with a few examples and have the students make conjectures based on what they see. I have outlined below some examples of graphs that will help the students understand. If you do not have access to Graphing Calculator then you can use the examples given, along with the movie, to demonstrate what will happen. Students should be able to look at the movie and explore the period of each graph by pausing the movie. Recall, the period=2pi/b. You may want to ask them what they expect to happen when b=0.

This is a picture of what will happen as the value of "b" changes. The graphs of each line are given below.

y= a sin(-3x+c)

y= a sin(-2x+c)

y= a sin(-1x+c)

y= a sin(1x+c)

y= a sin(2x+c)

y= a sin(3x+c)

Click Here To See What Happens as "b" Changes From -20 to 20

Exploring "c":

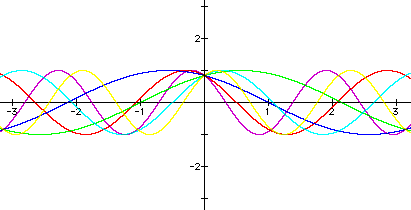
Once again, the effect changing "c" has on the graph is laid out in a manner that will help students understand the shift of the graph. Before starting, you may want to have the students predict what effect changing "c" will have on the graph. They may have to see a few examples before they realize that changing "c" simply shifts the graph along the x-axis.

This is a picture of what will happen as the value of "c" changes. The graphs of each line are given below.

y= a sin(bx-3)

y= a sin(bx-2)

y=a sin(bx-1)

y= a sin(bx+1)

y= a sin(bx+2)

y= a sin(bx+3)

Click Here To See What Happens As "c" Changes From -20 to 20 while a=3, b=3.

CONCLUSION:

As a follow up exercise, I suggest that you have the students play around with the cosine graph. After this exercise, they should be able to accurately predict how changing a, b, and c will effect the graph of y=a cos(bx+c). Depending on the level of your students you could also explore many other graphs and the effect that variables have on it.

Return to Kevin's Page