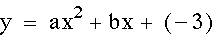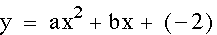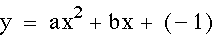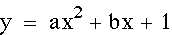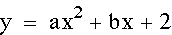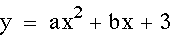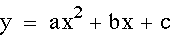
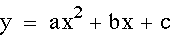
Below we will take a look
at how changing the variables a, b, and c will effect the graph
if the other two variables are held constant. It can be seen that
each variable has a tremendously different effect on the graph.
It is beneficial for your students to gain this understanding
on their own. I suggest graphing each equation seperately before
showing all of the graphs at once.
Exploring "a":
After observing the effects that varying 'a' can have on the graph of the equation we can see that the graphs of n and -n are 180 degree rotations, about the y-intercept, of each other. It is important to note that each of these graphs goes through the point (0,1). In other words, the y-intercept for each graph is 1. When we explore 'c' we will witness that c determines the y-intercept.
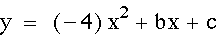
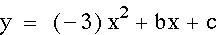
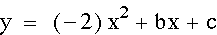
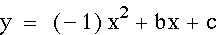
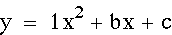
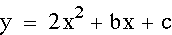
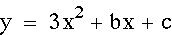
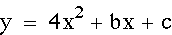
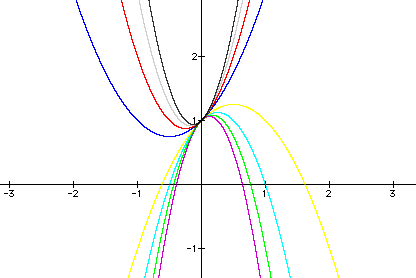
Special Note:
When a=0 we are left with y=x+1 which is simply the line with slope 1 and y-intercept 1. It is also the case that whenever a=0 the rest of the equation will yield a line. Here is a graph of the equation when a=0.
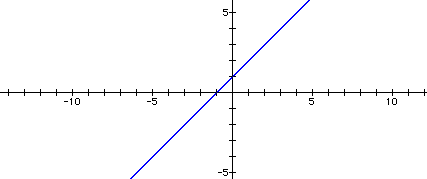
Exploring "b":
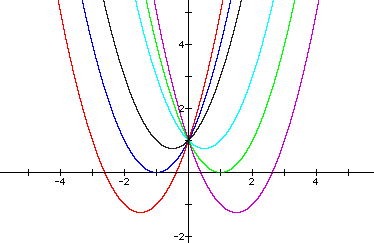
When 'b' varies while 'a' and 'c' are held constant the graph movies down as it moves to the right or left from the y-axis. As 'b' gets smaller the graph moves further to the right as it moves down. As 'b' gets larger the graph moves further to the left as it moves down. Also note, that the graphs for b=n and b=-n are mirrored across the y axis. Once again, note that each graph shares the same y-intercept.
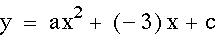
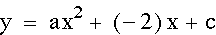
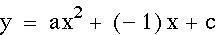
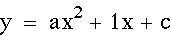
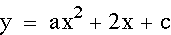
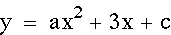
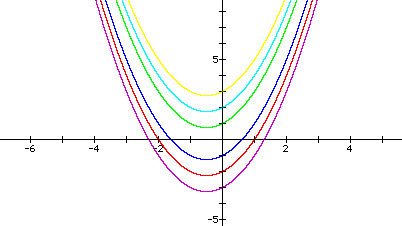
Above, when we were observing the effects of 'a' and 'b' we noticed that the y-intercept for each graph was the same. The reason for this is because the y-intercept is determined when x=0. So for these equations the y-intercept is equivalent to 'c'. In the graphs below, 'c' has been varied so that you can see how the y-intercept changes each time. Essientially, the graph is moved up and down as 'c' varies.