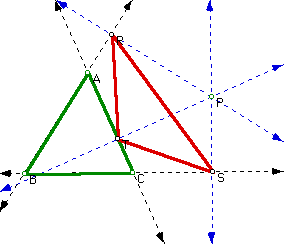
The Pedal Triangle
To create a pedal triangle you will start with a triangle ABC and point P. Create a line through each of the three pairs of vertices. Then construct a line perpendicular to each of these three lines and the point P. The points of intersection created by these perpendicular lines and the lines through the vertices can be connected to form the pedal triangle RST.

The Simson Line
After playing around with some possible positions for pedal point P it was interesting to note that if P is on the circumcircle of triangle ABC that the pedal triangle RST is actually not a triangle at all. In other words, it is a degenerative triangle because R, S, and T are all colinear. (For a GSP file of the path of the P on the incircle and circumcircle click HERE.) It is useful to look at this concept a little more in depth. In a situation such as this we call this degenerative triangle the Simson Line. In the picture below the Simson Line is shown in red.
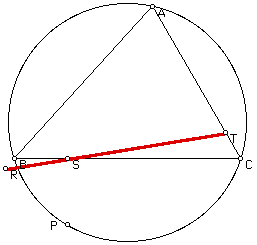
If you were to move P around the circumcircle you would discover that at three unique points the Simson Line is also one of the sides of the triangle ABC such as in the case below. The three unique times that this occurs is when P is one of the endpoints of the diameter of the circumcircle and one of the vertices of the triangle ABC is the other endpoint of the diameter. The diameter below is shown in dashed blue.
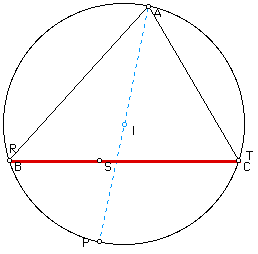
If we want the Simson Line to be the side BC then P needs to be the endpoint of the diameter with opposite endpoint at A. If we want the Simson Line to be the side AC then P needs to be the endpoint of the diameter with opposite endpoint B. And if we want the Simson Line to be the side AB then P needs to be the endpoint of the diameter with opposite endpoint at C. In general if we want P to be the point on the circumcircle such that the Simson Line is a given side of the triangle then P will be the point on the circumcircle such that the diameter with P as an enpoint also has the vertex of the triangle not on the desired side as the other endpoint of the diameter.