Jadonna Brewton

Fall 2000

Assignment #2

(Check out the assignment!!!)

 

Parabolas

of the form

We will begin with the most basic parabola with

a=1

b=0

c=0.

 

Notice that the vertex is at (0,0).

What does "a" do?

Look at a few graphs of equations that vary the value of a in the equation

a=1, -1, 2, 3, .5, 10, -.05

 

We immediately realize that a affects the width of the parabola as well as the direction that the the parabola opens (up or down). If a is negative, the the parabola opens downward. If a is positive, it opens upward.

As a gets larger, the parabola gets skinnier. As a gets smaller, the the parabola gets wider.

What does "c" do?

Next, look at some graphs of equations where a=1, b=0, and the value of c varies:

c= 0, 1, -1, 4, -4

 

 

It appears that c affects the vertical location of the vertex. When c is POSITIVE, the original vertex moves UP c units. When c is NEGATIVE, the vertex moves DOWN c units.

 

 

What does "b" do?

Now let's look at parabolas where a=1, c=0, and b varies.

b= 0, 2, -2, 4, -4

 

 

 

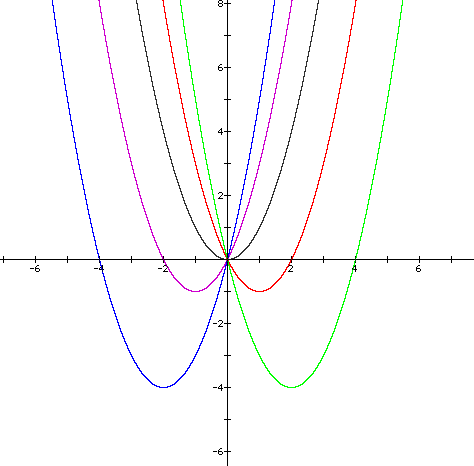
We notice that b also affects the location of the vertex. Recall that c affected the vertical location of the vertex. As the value of b varies from -4 to 4, there is a shift in the location of the vertex. When b is negative, there is a shift to the right. When b is positive, the shift occurs to the left. Also notice that there is a downward shift from the original parabola in both instances. Therefore, b affects both the horizontal and vertical positioning of the vertex.

It would be interesting to look at a continuous range of values of b.

 

This demonstrates how the graph of

changes with values of b ranging from -4 to 4. If we were to trace the path of the vertex, another parabola would be created. Click on the picture to see a demonstration of this.

 

But how do we know exactly where the vertex is at all times?

Let's sum up what we know about the graphs of

:

 

First, we let b=0 and c=0 while we varied a. We discovered that a affects the width and direction of the parabola.

Then we let a=1 and b=0 while we varied c. We discovered that c affects the vertical position of the vertex of the parabola

Then we let a=1 and c=0 while we varied b. We discovered that b affects the horizontal and vertical position of the parabola.

Let's look at a few more graphs and then we'll try to predict where the vertex is. Here the results are a little more interesting because we let b=1 and c=1 while we vary a. This is different because we are no longer looking at a parabola whose vertex is at (0,0). At first when we varied a while b=c=0, the vertex never changed positions; the width and direction of the parabola were the only changes. Now notice that the vertex also changes its location as we vary a. Notice that when a=0, you get the graph of a line that is tangent to all of the parabolas whose b and c are kept constant.

This indicates that the value of a also affects the location of the vertex.

 

a=0, .5, 1, 2, -2, 4, 10, -10

 

It turns out that the location of the vertex for a parabola in form

is

 

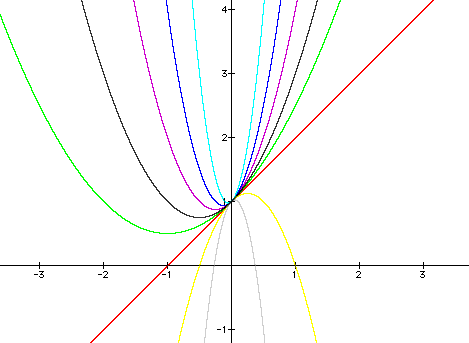
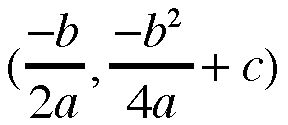
I personally did figure this out by trial and error!!! (HONESTLY). But then a friend, Nicole Mosteller, helped me justify this with a little more sophistication.

If you think of all the lines that are tangent to the parabola in the above form, you realize that there is one line whose slope is zero. The point of tangency for this particular line is the vertex. If we take the derivative of the quadratic equation above, we get

y'=2ax+b.

Recall that y' is the slope of the line tangent to the graph at a given point. We are interested in knowing what the cooordinates are when the slope, y', is equal to zero.

So we do a little bit of algebra and solve for x and y, the coordinates of the vertex:

 

 

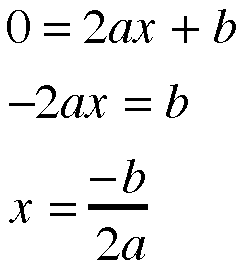
Now, solve for y by substituting for x in the original equation:

 

 

 

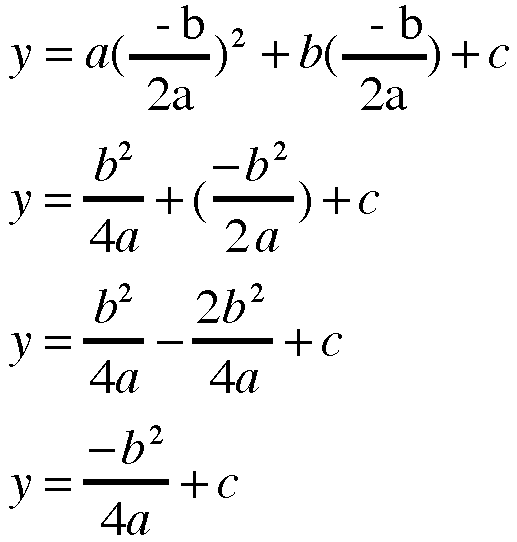
So, we have the coordinates of the vertex.

OTHER WRITE-UPS

RETURN TO JADONNA'S MAIN PAGE