Jadonna Brewton: EMAT6680/Fall2000/Assignment12

Jadonna Brewton

Fall 2000

Problem # 4

This write-up investigates the Fibonnaci Sequence where f(0) = 0, f(1) = 1, and f(n) = f(n-1) + F(n-2). There is also the Lucas Sequence where f(0) = 1 and f(1) = 3. You can also use Microsoft Excel to exlore other sequences that begin with any two integers you choose. Observe the charts of the sequences below and return to the disscussion.

The ratio of each pair of adjacent terms is given in the column labeled ratio first. Notice that the ratios converge to the Golden Ratio = 1.61803398874965.

The golden ratio is denoted as f. The exact value of the golden ratio is given below:

Here is a small proof that Dr. Wilson gave me to prove this:

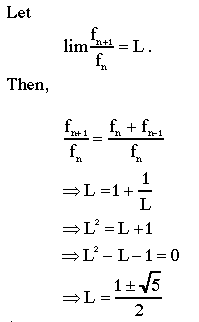Look at the limits of the ratios of every second, third, fourth, fifth, and sixth terms in the chart.

Here is a summary of the limits of these ratios:

Second

Third

Fourth

Fifth

Sixth

The proofs of the limits can be done using the proof above:

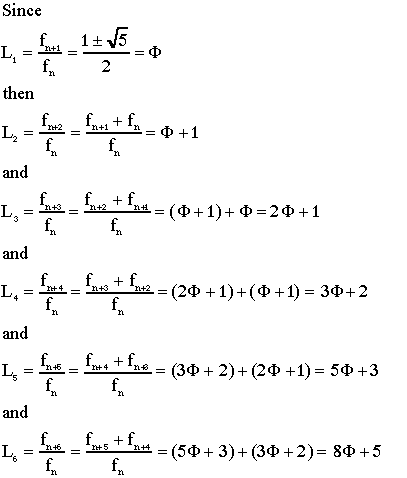
The proofs of the eqivalences of the powers of F begin a little like this:

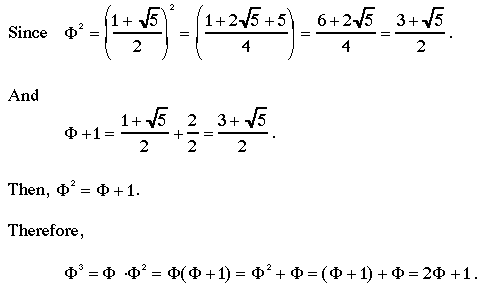
The other equivalences can be proven in a similar fashion.

OTHER WRITE-UPS

RETURN TO JADONNA'S MAIN PAGE

Fibonnaci Sequence

sequence	ratio	ratio	ratio	ratio	ratio	ratio
	first	second	third	fourth	fifth	sixth

1
1	1
2	2	2
3	1.5	3	3
5	1.66666666666667	2.5	5	5
8	1.6	2.66666666666667	4	8	8
13	1.625	2.6	4.33333333333333	6.5	13	13
21	1.61538461538462	2.625	4.2	7	10.5	21
34	1.61904761904762	2.61538461538462	4.25	6.8	11.3333333333333	17
55	1.61764705882353	2.61904761904762	4.23076923076923	6.875	11	18.3333333333333
89	1.61818181818182	2.61764705882353	4.23809523809524	6.84615384615385	11.125	17.8
144	1.61797752808989	2.61818181818182	4.23529411764706	6.85714285714286	11.0769230769231	18
233	1.61805555555556	2.61797752808989	4.23636363636364	6.85294117647059	11.0952380952381	17.9230769230769
377	1.61802575107296	2.61805555555556	4.23595505617978	6.85454545454545	11.0882352941176	17.952380952381
610	1.61803713527851	2.61802575107296	4.23611111111111	6.85393258426966	11.0909090909091	17.9411764705882
987	1.61803278688525	2.61803713527851	4.23605150214592	6.85416666666667	11.0898876404494	17.9454545454545
1597	1.61803444782168	2.61803278688525	4.23607427055703	6.85407725321888	11.0902777777778	17.9438202247191
2584	1.61803381340013	2.61803444782168	4.23606557377049	6.85411140583554	11.0901287553648	17.9444444444444
4181	1.61803405572755	2.61803381340013	4.23606889564336	6.85409836065574	11.0901856763926	17.9442060085837
6765	1.61803396316671	2.61803405572755	4.23606762680025	6.85410334346505	11.0901639344262	17.9442970822281
10946	1.6180339985218	2.61803396316671	4.23606811145511	6.85410144020038	11.0901722391084	17.944262295082
17711	1.61803398501736	2.6180339985218	4.23606792633341	6.85410216718266	11.0901690670006	17.9442755825735
28657	1.6180339901756	2.61803398501736	4.23606799704361	6.85410188950012	11.0901702786378	17.944270507201
46368	1.61803398820532	2.6180339901756	4.23606797003472	6.85410199556541	11.0901698158335	17.9442724458204
75025	1.6180339889579	2.61803398820533	4.23606798035119	6.85410195505207	11.090169992609	17.9442717053337
121393	1.61803398867044	2.6180339889579	4.23606797641065	6.85410197052679	11.0901699250868	17.9442719881744
196418	1.61803398878024	2.61803398867044	4.2360679779158	6.85410196461598	11.090169950878	17.9442718801389
317811	1.6180339887383	2.61803398878024	4.23606797734089	6.85410196687371	11.0901699410266	17.9442719214048
514229	1.61803398875432	2.6180339887383	4.23606797756049	6.85410196601133	11.0901699447895	17.9442719056426
832040	1.6180339887482	2.61803398875432	4.23606797747661	6.85410196634073	11.0901699433522	17.9442719116632
1346269	1.61803398875054	2.6180339887482	4.23606797750864	6.85410196621491	11.0901699439012	17.9442719093635
2178309	1.61803398874965	2.61803398875054	4.23606797749641	6.85410196626297	11.0901699436915	17.9442719102419

return to disscussion of limits

Lucas Sequence

SEQUENCE RATIO RATIO RATIO RATIO RATIO RATIO

FIRST SECOND THIRD FOURTH FIFTH SIXTH

1

3 3

4 1.33333333333333 4

7 1.75 2.33333333333333 7

11 1.57142857142857 2.75 3.66666666666667 11

18 1.63636363636364 2.57142857142857 4.5 6 18

29 1.61111111111111 2.63636363636364 4.14285714285714 7.25 9.66666666666667 29

47 1.62068965517241 2.61111111111111 4.27272727272727 6.71428571428571 11.75 15.6666666666667

76 1.61702127659574 2.62068965517241 4.22222222222222 6.90909090909091 10.8571428571429 19

123 1.61842105263158 2.61702127659574 4.24137931034483 6.83333333333333 11.1818181818182 17.5714285714286

199 1.61788617886179 2.61842105263158 4.23404255319149 6.86206896551724 11.0555555555556 18.0909090909091

322 1.61809045226131 2.61788617886179 4.23684210526316 6.85106382978723 11.1034482758621 17.8888888888889

521 1.61801242236025 2.61809045226131 4.23577235772358 6.85526315789474 11.0851063829787 17.9655172413793

843 1.61804222648752 2.61801242236025 4.23618090452261 6.85365853658537 11.0921052631579 17.936170212766

1364 1.61803084223013 2.61804222648752 4.2360248447205 6.85427135678392 11.0894308943089 17.9473684210526

2207 1.61803519061584 2.61803084223013 4.23608445297505 6.85403726708075 11.0904522613065 17.9430894308943

3571 1.6180335296783 2.61803519061584 4.23606168446026 6.85412667946257 11.0900621118012 17.9447236180905

5778 1.61803416409969 2.6180335296783 4.23607038123167 6.85409252669039 11.0902111324376 17.944099378882

9349 1.61803392177224 2.61803416409969 4.23606705935659 6.85410557184751 11.0901542111507 17.9443378119002

15127 1.61803401433308 2.61803392177224 4.23606832819938 6.85410058903489 11.0901759530792 17.944246737841

24476 1.61803397897799 2.61803401433308 4.23606784354448 6.85410249229908 11.0901676483915 17.9442815249267

39603 1.61803399248243 2.61803397897799 4.23606802866617 6.85410176531672 11.0901708204985 17.9442682374264

64079 1.61803398732419 2.61803399248243 4.23606795795597 6.85410204299925 11.0901696088612 17.9442733127975

103682 1.61803398929446 2.61803398732419 4.23606798496486 6.85410193693396 11.0901700716654 17.9442713741779

167761 1.61803398854189 2.61803398929446 4.23606797464839 6.8541019774473 11.0901698948899 17.9442721146647

271443 1.61803398882935 2.61803398854189 4.23606797858893 6.85410196197258 11.0901699624122 17.9442718318239

439204 1.61803398871955 2.61803398882935 4.23606797708378 6.85410196788339 11.090169936621 17.9442719398595

710647 1.61803398876149 2.61803398871955 4.23606797765869 6.85410196562566 11.0901699464723 17.9442718985935

1149851 1.61803398874547 2.61803398876149 4.23606797743909 6.85410196648804 11.0901699427094 17.9442719143557

1860498 1.61803398875159 2.61803398874547 4.23606797752297 6.85410196615864 11.0901699441467 17.9442719083351

3010349 1.61803398874925 2.61803398875159 4.23606797749093 6.85410196628446 11.0901699435977 17.9442719106348

4870847 1.61803398875014 2.61803398874925 4.23606797750317 6.8541019662364 11.0901699438074 17.9442719097564

top of page

OTHER WRITE-UPS

RETURN TO JADONNA'S MAIN PAGE