Investigation of the Proof of the Ratio
(AF)(BD)(CE) to (BF)(CD)(AE) equals 1.
by
Kimberly Burrell
After making the conjecture that the ratio of (AF)(BD)(CE) to (BF)(CD)(AE) is always equal to 1 no matter the location of point P, some proof will be required.
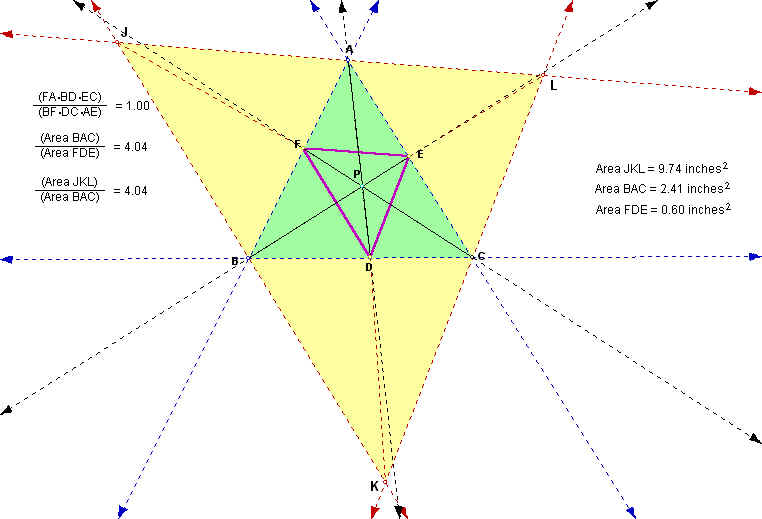
In order to begin we must construct lines parallel to segment FD through B, to FE through A, and to segment DE through C. Points of intersection between these parallel lines are required (J, K, and L). We will now construct line segments JF, DK, and LE as shown below in the illustration.
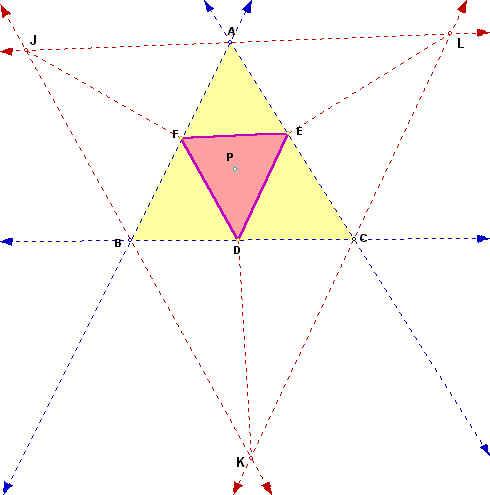
At time we are interested in triangles BJA, KBC, and ALC; in particular the ratio of the area of purple triangles to the green triangles as shown.
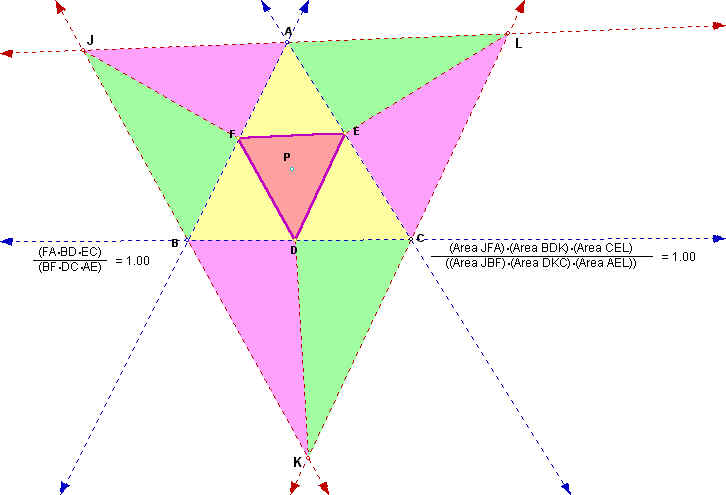
One can observe that in the above illustration that the ratio of interest is equal to 1, with is just as the primary ratio being investigated. Please click here to see if this relationship holds true for any location of P.
At this time, we feel it would be interesting to compare the ratio of area of triangles JKL and ABC to the ratio of areas of triangles ABC and FED. One can observe from the following illustration that the ratios are equal. This is true for all locations of P.