

Investigating a point P that is inside a given triangle ABC.
by
Kimberly Burrell
PROBLEM: Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
In order to begin our investigation, we must first illustrate the problem.

As we begin to investigate our problem, we will first examine the ratio of (AF)(BD)(CE) to (BF)(CD)(AE). After moving P to possible positions inside triangle ABC, we find the ratio to be 1. To receive a greater comprehension of this ratio, we will break it into smaller components. Here, we find that the product of any pair of smaller ratios is the mutliplicative inverse of the remaining ratio. Click here to explore this for yourself.

To investigate the proof of this, click here.
What will happen if we make the sides of triangle ABC lines instead of segments and place the point P outside triangle? We have chosen to place P as shown in following GSP sketch.

As with the previous portion of this problem, the ratio of (AF)(BD)(CE) to (BF)(CD)(AE) remains 1. The product of the smaller ratio components remains the multiplicative inverse of the other ratio.
Now, we will concentrate on the areas of the triangles. One triangle is our given triangle ABC, and the other triangle is formed by the intersecting lines of P and triangle ABC, known as triangle DEF. The ratio of the areas of triangle ABC to triangle DEF is always greater than or equal to 4. The ratio is 4 when point P is the centroid of triangle ABC. This fact has several ways that it can be confirmed. By moving point P to a position such that the ratio is 4, one can observe that AP is two-thirds of AD, CP is two-thirds of CF, and BP is two-thirds of BE. Likewise, we can check to see that F, D, and E are the midpoints of AB, BC, and AC, respectively. To check the assertion that the ratio is 4, find the areas of triangles BED, FED, AEF, and CED. They should be equal, and each one would be one-fourth of the area of triangle ABC.
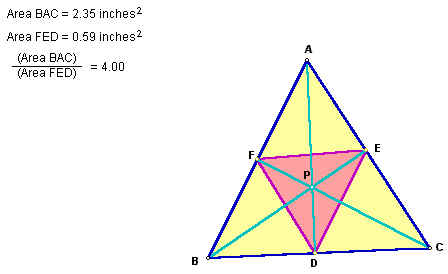
Click here to explore this for yourself.