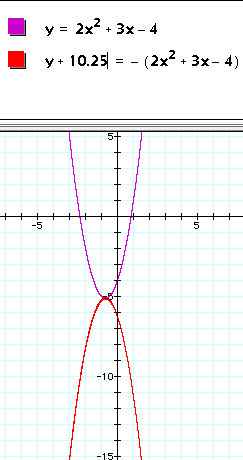
Making the y-values opposite in order to make the parabola concave down is the easy part. We simply have to multiply all of the y-values by -1.

The hard part is shifting the
vertex so that it lies on the vertex of the original graph. We
have options here. We can complete the square in order to find
the vertex form of our equation. We can also take a shortcut to
find the vertex of the equation. Let's take the shortcut. The
x-value of the vertex of a parabola whose equation is ![]() can be found using the equation
can be found using the equation ![]() . In
this case, we have
. In
this case, we have ![]() . Now we can use
this x value in our equation
. Now we can use
this x value in our equation ![]() in
order to find the y coordinate of the vertex. The work follows:
in
order to find the y coordinate of the vertex. The work follows:
so
Notice the symmetry in our graphs
above. The y-value of the vertex of our original purple graph is ![]() .
.
The y-value of the vertex of
our flipped red
graph is ![]() (You should verify this). In order to shift
the red graph down so that its vertex conincides with the vertex
of the purple graph, we will have to shift it down
(You should verify this). In order to shift
the red graph down so that its vertex conincides with the vertex
of the purple graph, we will have to shift it down ![]() =
=
![]() = 10.25 units. Here is the equation and the
graph of the solution.
= 10.25 units. Here is the equation and the
graph of the solution.