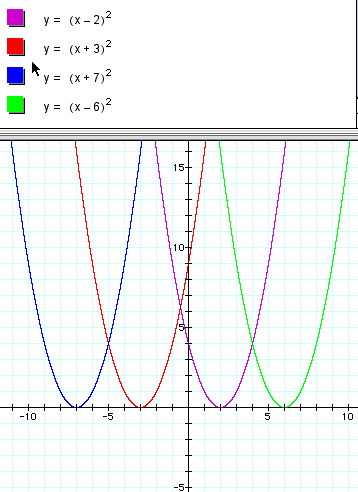
Did you find that the graph appears to shift horizontally along the x-axis? If you look at the x value of the vertex of each graph, it corresponds to the numerical value in the parentheses. Furthermore, if you look at the signs in the parentheses, they seem to be the opposite of the x-value of the vertex. For example, in the purple graph, the (x-2) seems to move the vertex of the graph to the coordinate (2,0), while the (x+3) seems to move the vertex of the graph to the coordinate (-3,0). In fact, if you find the value of the independent variable (x) that makes the argument (the stuff being squared here) equal to zero, this will give you the magnitude AND the direction of the horizontal shift.
Let's get a little more complicated
for a moment. Take, for example the function 
.
If we want to find the magnitude and direction of the horizontal
shift of the parent function, we can solve the equation 3x-17=0.
Doing so, we find x=17/3 or positive five and two thirds. This
would indicate a shift to the right five and two thirds units.
Below is a graph of this function.
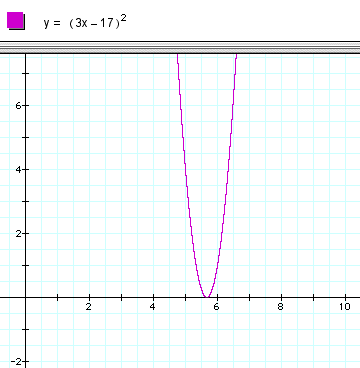
Do you notice any other change in the parabola as we compare it to the parent function?
We will address horizontal stretches and compressions at another time.
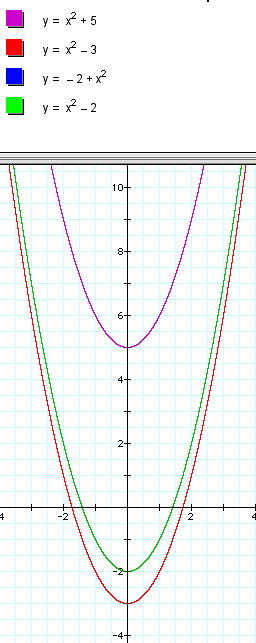
Did you find that the graphs shifted vertically? Notice that the vertex of the purple graph is at (0,5) and the entire graph of the parent function appears to have slid up 5 units. Looking at the red graph, the entire graph appears to have slid down 3 units. Take some time to compare these results with your previous results that led to a horizontal shift. Write down some rules that will help you remember which number does what and which direction the graph is shifting.
Did you notice that the latter two graphs (blue and green) were identical? What mathematical property of real numbers makes this so?