

Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides at points D, E, and F respectively.
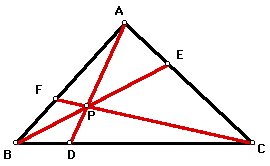
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P. Click here for a GSP sketch that can be manipulated.
Can the result be generalized (using lines rather than segments to construct ABC) so that point P can be outside of the triangle? Click here for a working GSP sketch. Can you prove the general case?
Finally, show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. Click here for a GSP sketch. I leave the proof to you again.
When is it equal to 4. Answer.