:Prove that (AF)(BD)(CE)=(BF)(CD)(AE), and :
Given AD, BE, and CF are concurrent at point P, construct a line parallel to BC, through A and extend CF and BE to intersect this line at G and H respectively.
From the above diagram, we can establish angle AGP congruent
to angle DCP, and angle GAP is congruent to angle CDP because
alternate interior angles are congruent. So triangle GAP is similar
to triangle CDP by angle-angle. Therefore, 
because corresponding sides of similar triangles are proportional.
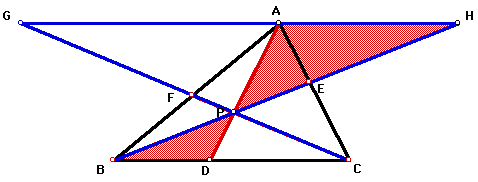
From the above diagram, we can establish angle AHP congruent
to angle DBP, and angle HAP is congruent to angle BDP because
alternate interior angles are congruent. So triangle HAP is similar
to triangle BDP by angle-angle. Therefore, 
because corresponding sides of similar triangles are proportional.
By substitution, 
, or 
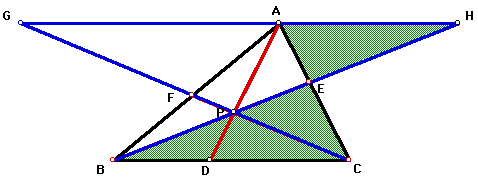
From the above diagram, we can establish angle AHE congruent
to angle CBE, and angle HAE is congruent to angle BCE because
alternate interior angles are congruent. So triangle AEH is similar
to triangle CEB by angle-angle. Therefore, 
because corresponding sides of similar triangles are proportional.
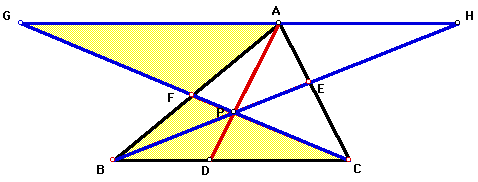
From the above diagram, we can establish angle GAF congruent
to angle CBF, and angle AGF is congruent to angle BCF because
alternate interior angles are congruent. So triangle GAF is similar
to triangle CBF by angle-angle. Therefore, 
because corresponding sides of similar triangles are proportional.
So 
by the multiplicative property
of equality. Furthermore, 
by
the property of multiplicative inverses. Therefore 
by the transitive property, or 