

The graphs of polar equations show particular functions that many people find both interesting and curious as well. This investigation involves equations of the form
where a, b and k are real numbers. As equations in polar form tend to be a bit confusing (at least to me anyway) I choose to begin this investigation by viewing some equations of a simple form. Consider the diagram below.
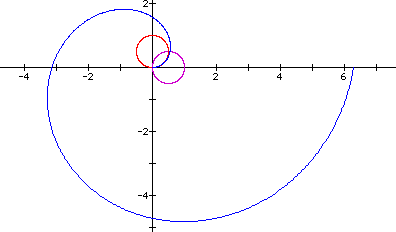
Here the graph created by each of the different equations may be seen. Recalling that theta is an angle in radian measure and varies from 0 to 2pi allows for greater understanding of the diagram.
Next, I begin to look at some different polar equations of greater complexity.
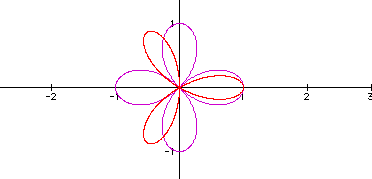
When k is even, the graph always has 2k petals; however, when k is odd the graph contains only k petals. To access the document used to create the diagram show, click here. Once you have downloaded the Graphing Calculator file, experiment with different k values to determine if my statement is true, or simply believe me.
Now let's take the next step and multiply the cos function by a constant, b. See below for some examples.
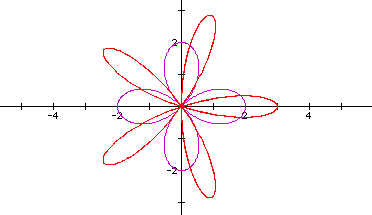
I purposely chose to not label the equations with the color of their graph. Having read the previous statements it should be apparent which graph represents which function. If not, click here to access the file which created the above image. A second way to determine which graph relates to a particular function is to consider the effect of multiplying by 2 or 3. Since each petal of the purple graph stretches to 2, it may be inferred that multiplying the function by a constant will force the petals to stretch (or shrink) to that value.
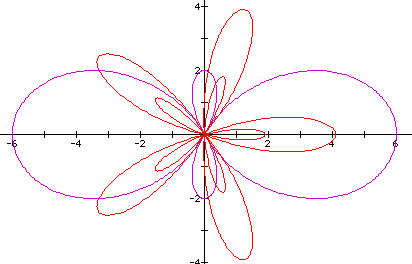
The next step will be to consider functions of the above type with a constant added to them. View several examples below. Click here to access the file used to create the image below.
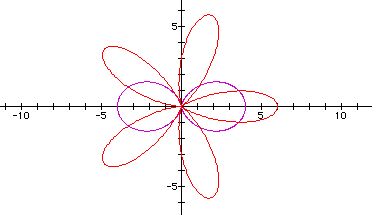
The first observation I make is that theta being multiplied by an even number, k, no longer produces 2k petals. Also, note that adding a constant to the functions stretches the petals by an amount equal to this value. Another characteristic to notice is that I have chosen to add the same number as cos was multiplied by. See below to find out what happens when a different number is chosen for the value of a.
Now it becomes truly interesting. Click here to access the file used to create the image above. I highly recommend the reader experiment with different values of a and b so as to see other producible images.
Here I look at equations of the general form
where a and k are constants and b is allowed to vary. To access the file, click here.
Next I let b and k be constants and allowed a to vary. Click here for access to that file.
Finally I decided to see what would occur if a and b were held constant and k was allowed to vary. This is by far the most outrageous of the bunch, in my opinion. Click here to access that file. Really, click the link it is worth a look.
As a note to the reader, the files above have different values for the constants. I did this mainly for the sake of my interest. If I was to present this material to a class, I would definitely choose to let each of the constants be the same value in each application. I did however remain consistent in the values on which the variable was defined. In each case, I let the slider run from -10 to 10 and had it take 100 steps.
In conclusion, this form of a function is rich with possibilities for investigation. For example, one may change the cos function to sin and see that the related graphs are all rotated 90 degrees about the origin. Also, by considering adding or subtracting values from theta, more differing graphs may be created.