

It has now become a rather standard exercise, with available technology, to construct graphs to consider the equation
and to overlay several graphs of
for different values of a, b, or c as the other two are held
constant. From these graphs discussion of the patterns for the
roots of
can be followed. Let's now look at graphs of this equation as we allow a, b, and c to vary. For example, if we set
for a = -3, -2, -1, -0.5, -0.25, -0.1, 0, 0.1, 0.25, 0.5, 1, 2, 3, and overlay the graphs, the following picture is obtained.
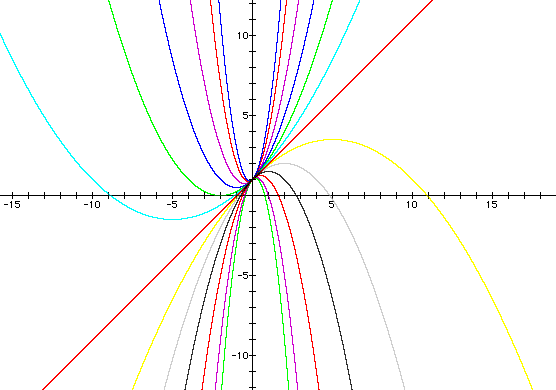
Here the author has deliberately chosen to leave out any labeling to enable a teacher to use this web site for instruction in a classroom environment. Understanding there are both many curves in this visual representation and the fact that we as teachers generally like to have an answer key for at least some of the questions which we ask our students, find here a link to the Graphing Calculator 3.0 document which created the figure shown. This will allow the teacher to remove some of the curves as well as help students to comprehend which equation describes a particular curve.
For discussion we also wish to consider the equation
where a = -3, -2, -1, -0.5, -0.1, 0, 0.1, 0.25, 0.5, 1, 2, 3 and overlay the graphs of the curves that will be created. The following picture is obtained.
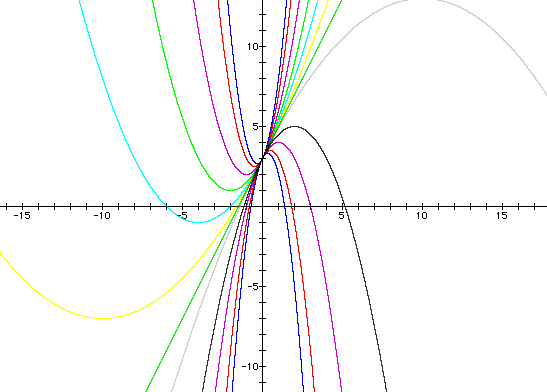
Again find the document from Graphing Calculator 3.0 which created this picture here. At this point either students will question why the curves appear to be different or the teacher should pose the question. It may lead to the discussion of what happens when b and c in the general quadratic equation vary.
Below see some examples of curves created when b varies. We first consider the equation
when b= -3, -2, -1, -0.5, 0, 0.25, 1, 2, 3. View the graph below. Which curve is not represented by an equation of the above form? Access the document which created the image below here.
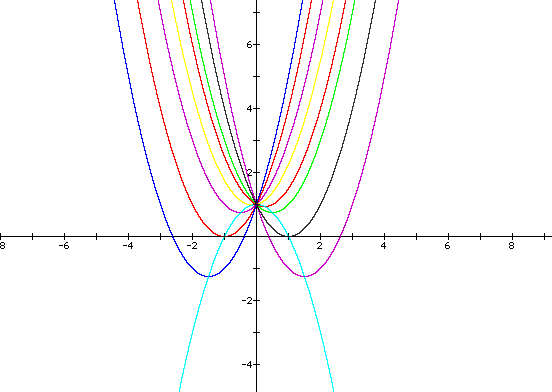
The parabola which is concave down contains each of the vertices of the other parabolas. What is its equation? Below find the graphs of equations of the form
where b = -4, -2, -0.5, -0.1, 0.5, 1, 2, 3. Access the document which created the image here.
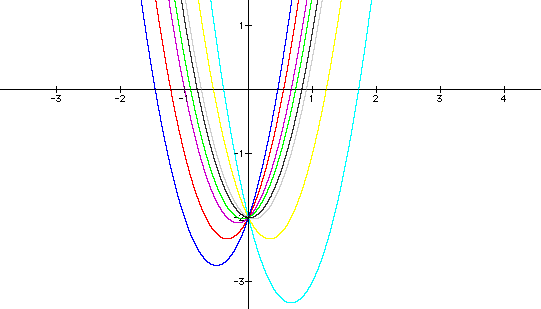
Can you find the equation of the parabola that would pass thru the vertices of each of the parabolas of the above form?
Hopefully now some hypotheses of what occurs when c varies are forming in the minds of your students. Let's view some specific cases. First consider the equation
where c = -2, -1, -0.25, 0.5, 1, 2, 4. Below is the image created in Graphing Calculator 3.0 when the equations are graphed. Click here to access the document itself.
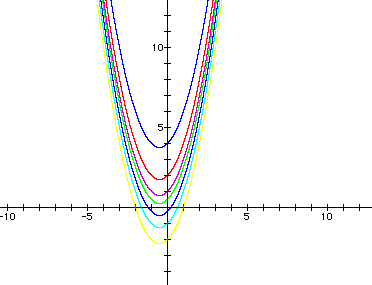
After discussing what effect changing the values of c has on the graphs, consider the equation
to add more to your class's discussion. The graph below shows the parabolas of the above form when c = -4, -2, -1, -0.25, 0.25, 1, 2, 4. Click here to access the document used to create the figure below.
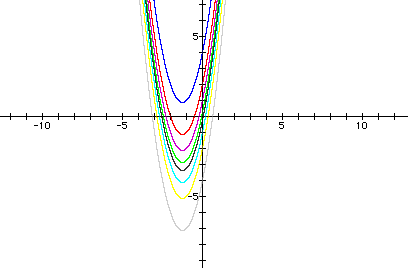
Having lead your class to understand that changing a, b, or c in the general quadratic equation changes the parabola in different ways, you may extend the investigation to consider the roots of the various parabolas. Engage your students so as to allow them to recall that the roots of an equation are the points where the graph intersects the x-axis. In the graphs above it is quite easy to determine the roots for the different parabolas. We would like to take this idea one step further and examine the graphs in different coordinate planes, these being the xa plane, the xb plane, and the xc plane. It is essential that the student understand what these different planes are and how graphing works in them.
In this author's opinion explaining that allowing the constant a to be replaced with the variable y will yield a graph in the xa plane as opposed to the xy plane is enough teacher direction to allow the discussion of the different planes to begin. Your students should understand how the xb and xc planes are acquired before continuing.
Let's first consider:
In order to have an equation in the xa plane, it must be of the form
Here we have a=y, b=1, and c=1. These values relate to those in this graph. Below you will find the graph of the above equation as well as the graphs of a=3 and a=-2. (Note to enable Graphing Calculator 3.0 to graph the two horizontal lines we must enter y=3 and y=-2. You may see this when clicking here to access the document which created the graph below.)
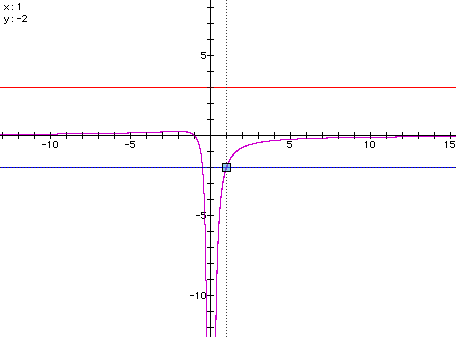
Looking at the intersection points of the horizontal lines and the curve we see the roots of the parabola for a = the value of the horizontal line. For example in the figure above a = -2 intersects the given curve at x = 1. This is one root of the equation
where a = -2. What is the other root of this parabola? Another question to pose to your students is what must be true since the line a = 3 does not intersect the curve. For a visual reference look below. To link to the document which created the image below, click here. To be certain that everyone understands which equation represents which curve refer to the key below. (Note that y in the first equation is the same as a in the equation above. I had to "trick" the grapher.)
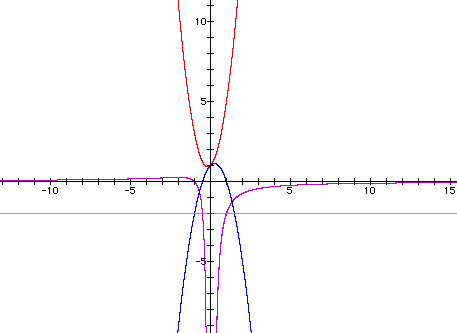
Your students should be able to explain that the red graph, where a = 3, does not intersect the x-axis and therefore has no real roots. Thus in the xa plane the line a = 3 never intersects the purple graph. Here lead your students to recall that a quadratic has one real root if the vertex of the parabola is on the x axis. An investigation they may do is to find what value of a gives only one real root. How could they use the ideas expressed about the xa plane to find the answer to this question? To view a graph which shows the answer to this question, click here.
Here we wish to change our thinking to consider
Now we must use the equation
in order to be in the xb plane. Note that here a=1, b=y, and c=1. The image below shows the graph of the above equation as well as the lines b=8 and b=-2 in the xb plane. To access the document used to create this image, click here.
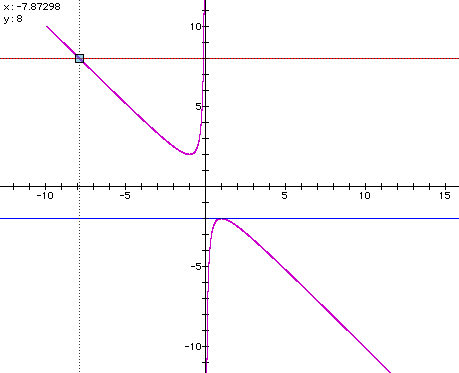
Engaging your students to see if they understand what significance the intersection shown above has will allow you to see if they grasp this relationship between the roots of various polynomials. By looking at the figure above, one should be able to state what value of b yields a parabola with vertex on the x-axis when both a and c are one. Another question worth asking is what happens to the values of the roots as b gets very large or very small. Click here for my answer.
Finally let us look at
In the following example the equation
is considered so as to not develop the rut that all the constants are always one. If the equation is graphed in the xc plane, it is easy to see that the curve will be a parabola (view the figure below or click here for access to the document used to create this graph).
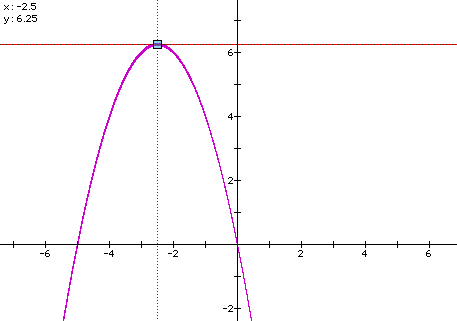
For each value of c considered, its graph will be a line crossing the parabola in 0, 1, or 2 points -- the intersections being at the roots of the orignal equation at that value of c as discussed earlier in the xa and xb planes. Having earlier considered these two planes, the hope is that your students will understand that there is one value of c where the equation will have only 1 real root -- at c = 6.25. For c > 6.25 the equation will have no real roots and for c < 6.25 the equation will have two roots, both negative for 0 < c < 6.25, one negative and one 0 when c = 0 and one negative and one positive when c < 0.
Using any of the linked documents to adjust values and thereby
gain new graphs may be interesting to your students and will allow
you to determine their comprehension of the general quadratic
and its roots.
Send e-mail to jklerlei@coe.uga.edu to reach (soon to be Dr.) Klerlein