Assignment #4

The following write-up will be an examination of the circumcenter of a triangle. First, we start with a definition of the circumcenter of a triangle. Click here for a diagram.

The circumcenter of a triangle is the point equidistant from the three vertices. We can see that each vertex can be moved so the circumcenter can be inside, outside, or on the triangle. All variations of diagrams show the circumcenter exists and is one point. Click here for movable diagram. Note the circumcenter is inside an acute triangle, on the side of a right triangle, and outside an obtuse triangle.

It remains to prove the circumcenter is exactly one point.

The circumcenter is the intersection of the three perpendicular bisectors. We know two lines intersect in either no points, one point, or infinitely many points. For the lines to intersect in infinitely many points, the lines must be scalar multiples of each other. Thus, they must be parallel. This would imply the sides of a triangle are parallel. We know this cannot be true. Click here for quick proof. Thus, the circumcenter is at most one point. We now need to see there must be one point that is the circumcenter. Assume the triangle ABC is as shown.

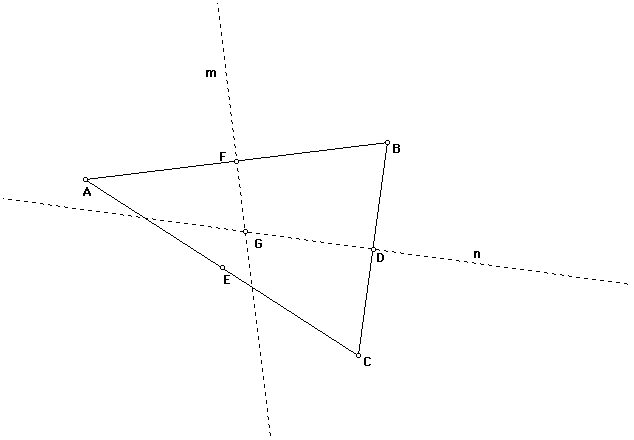
We know the perpendicular bisectors of BC and AB intersect in one point, G, (because they are not parallel.) This point G is equidistant from points A and B and points B and C. Thus, point G is equidistant from points A and C and so, it is on the perpendicular bisector of AC. Therefore, all three perpendicular bisectors are concurrent. Every triangle must have exactly one circumcenter.