Assignment 4: Proof a triangle cannot have parallel sides

Assume there is a triangle with parallel sides. On the triangle below, side AB and BC are parallel.

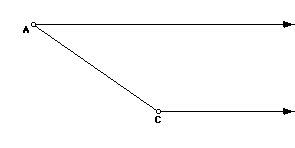
For this to occur, there exists some point B that is on both parallel sides. Thus, AB is parallel to BC. By definition of parallel lines, two parallel lines that intersect the same point are linear multiples of each other. So, points A, B, and C are co-linear. This contradicts the fact that A,B, and C form a triangle.