---

Lesson 6: Area of regular polygons

---

By: Tim Lehman

---

Students will now combine what they have learned about area and the Pythagorean Theorem. They will find the area of different regular polygons.

The students first need to construct the regular polygons on GSP. A hexagon is a good place to start. After constructing the hexagon, its area should be found. First, we can see the hexagon can be divided into six congruent triangles. The triangles are also equilateral. How do we know they are equilateral?

If the area of the triangles can be found, then the area of the hexagon will immediately follow. Because the triangles are equilateral, all of their sides are equal. Let's assume the length each side of the hexagon is 1 unit.

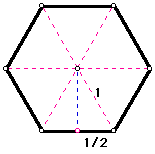
By using the Pythagorean Theorem, we can find the height (in blue) of the triangle and, thus, the area of the hexagon. Click here for a GSP sketch of a hexagon.

Students with an understanding of trigonometry can then go on to work on other polygons. For those who do not, the students can be provided a trig table or be provided the lengths needed. This would still leave the challenge of constructing the polygons (click here for an octogon with construction lines and here for one without) and applying the theorem.