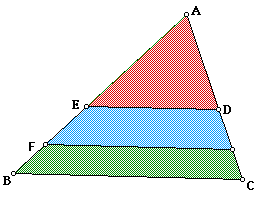
Where would this segment be?
By: Tim Lehman

After constructing a line parallel to a side that forms a triangle equal to one third of the area of the original triangle, it remains to find the segment that divides the remaining portion of the triangle (trapezoid EDCB below) in half.
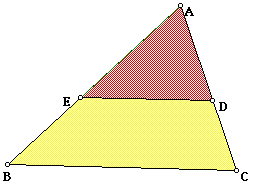
Thus, we want to find point F on AB such that the ratio of the length of the segment AE to segment AB is square root of 2 divided by square root of 3 to 1. From our previous work, we know that the ratio of AE to AB is 1 divided by the square root of 3 to 1. Thus, the ratio of AE to AF is 1 to square root of 2. Because the ratio of the legs to the hypotenuse of a 45-45-90 triangle is 1 to the square root of 2, we only need to construct a 45-45-90 triangle with leg length AE and the length of the hypotenuse will be the distance of A to F.
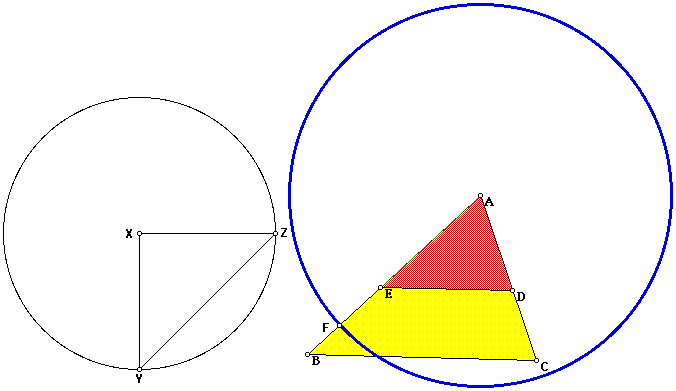
In the diagram above, segments XY, XZ, and AE are all equal in length. Angle YXZ is a 90 degree angle. Thus, XYZ is a 45-45-90 triangle, as desired. The blue circle is centered at A with a radius the same length as YZ. Therefore, the distance from A to F is the same as Y to Z. Therefore, F is the point we are looking for on AB. Construct segment FG such that FG is parallel to ED and BC. The original triangle is now divided into three pieces of equal area.