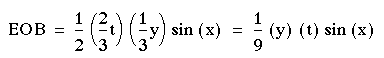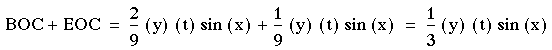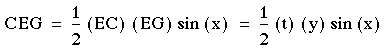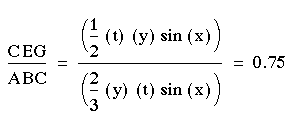This time the construction has to be done more carefully. For better investigation, let the two triangle not be separetely constructed as earlier. Now construct triangle ABC as shown in the figure below. Let CE, BD and AF be the medians of triangle ABC. Using median CE and point E construct a ray parallel to DB and also construct another ray from C, parallel to CB to meet the other ray at point G. Using points CEG construct segments to form triangle GEC as shown below. Click here to see gsp file
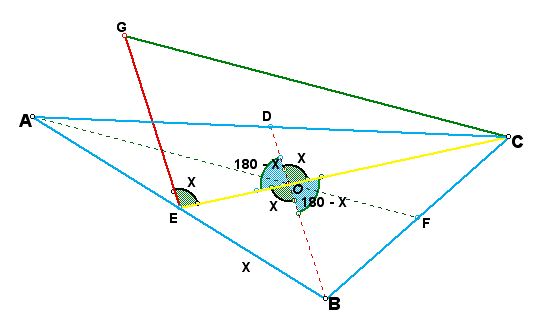
Note that as per the construct, segment GE is paralle to DB, and AF is parallel to CG, taking EC as the transversal line, angle GEC is corresponding to DOC, hence equal. Let angle GCE be X degrees, angle DOC will be supplimentary to BOC hence angle BOC will be (180 - x)º. With the same arguement, angle EOB will Xº.
Before I go further to proof this conjecture, it should be noted that medians have two main properties
With that in mind, let us
consider triangle ABC and median EC which devide it in two equal
areas. Therefore area EBC is = 
.
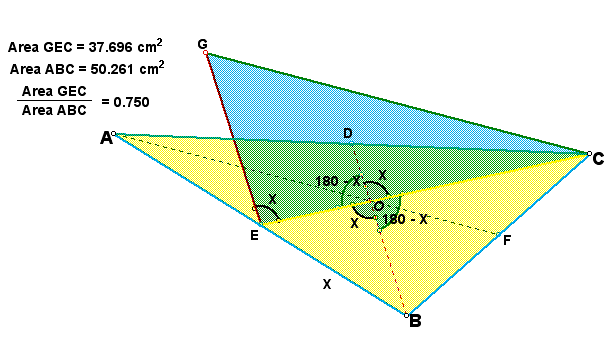
I will find the area of triangle EBC which
is area of triangle EOB + area of triangle BOC. To find area of
a triangle, I will use the formula 
where
a and are sides that enclose the angle.
Area of triangle 
Area of triangle 
Now let EC = y and DB = t, then using property (i) then OC = 2/3EC = 2/3y, where as OB = 2/3DB = 2/3t
therefore area of triangle
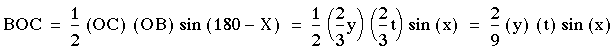
and area of triangle
