Here is the problem
Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. (E.g., are they congruent? similar? have same are? same perimeter? ratio of area? ratio of perimeter?) Prove whatever you find.
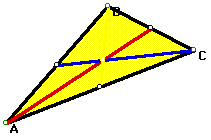
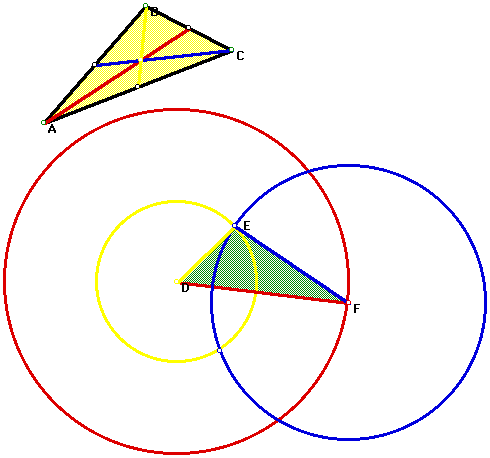
First let us construct a triangle ABC as shown below. Note that to make things easy for discussion, we will color each median a different color. Then construct a different triangle with the sides equal to the medians of the original triangle. This can be

by first picking a point and highlithing one of the median and then construct a circle (note that the radius will be the length of the median). Do the same to the other points shown below.(click script)
After exploration with with
the geometric sketch, I was concern with the area of triangle
ABC and area of a triangle made of median. I observed that the
area of the new triangle is 75% of the original triangle. To confirm
what I'm demonstrating click here for animation or click here and see for yourself . It can be noted that as the
dimension of ABC changes, all other measurement of the two triangles
changes but the ratio of the areas does not change. The ratio
remains to be 75% throughout as the dimension of ABC changes.
Click her for the proof
Back to Samuel's page