Day7

EMAT 6690

~ Centroid ~ Incenter ~

For the next two days we will explore points of concurrency. The point of concurrency is the point where concurrent lines intersect. This is a single point.

Materials needed for this lesson are wax paper, straightedge, and pencil.

Students will need to have access to Geometer's Sketchpad.

A triangle has many special lines: medians, angle bisectors, perpendicular bisectors, and altitudes to name a few. Each triangle has three of the previously mentioned lines.

A median is a line drawn from a vertex to the midpoint of the opposite side. The point of concurrency of the medians is called the centroid of the triangle.

Investigations that can be used as teaching tools for the centroid.

Investigation #1

Step 1 On a sheet of paper or wax paper, draw a large scalene acute triangle. Make the triangle as large as you can.
Step 2 Fold to construct the three medians of each side of the triangle. *Bring the endpoints together and pinch to locate the midpoints, then construct the medians with your straightedge.
Step 3 Repeat steps 1 and 2 for an obtuse scalene triangle.

Investigation #2

Step 1 Take the scalene acute triangle you constructed in the previous investigation and label it ABC, as shown below. Do not worry if your triangle is a different shape.

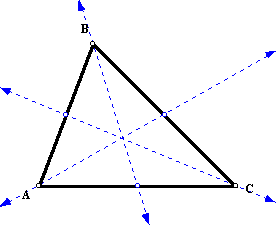
Step 2 Label the three medians AF, BD, and CE. Label the centroid G.

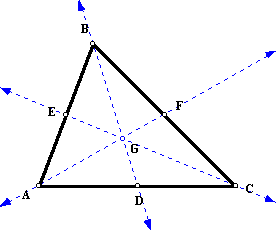
Step 3 Use your compass to answer the following questions: Is the centroid the same distance from the vertices? From the three sides? Take a look at how the centroid divides each median into two parts. Is the centroid the midpoint of each median?
Step 4 You should have answered no to each question in Step 3. Now compare the small part on each median to the big part on that median. With you compass or another piece of wax paper, measure GF. Compare GF with AG by seeing how many times you can mark off the distance GF on AG. (If, for example, you can mark off GF three times on AG, then AG is three times as long as GF.) How many times as long as GF is AG?
Step 5 Compare the lengths of the parts of the other two medians. (Segment BG is how many times as long as GD? Segment CG is how many times as long as GE?)

Students should be able to complete the follow conjecture after completing the student activity with Geometer's Sketchpad.

The centroid of a triangle divides each median into two parts so that the distance from the centroid to the vertex is -(twice)- the distance from the centroid to the midpoint.

An angle bisector is a ray that divides an angle into two congruent angles. The point of concurrency of the angle bisectors is called the incenter of the triangle.

Investigations that can be used as teaching tools for the incenter.

Investigation #1

Step 1 On a sheet of paper or wax paper, draw a large scalene acute triangle. Make the triangle as large as you can.
Step 2 Fold to construct the three angle bisectors in each angle of the triangle. *At each the vertex of the triangle pinch to locate the position of the angle bisector, then construct the angle bisectors with your straightedge.
Step 3 Repeat steps 1 and 2 for an obtuse scalene triangle.

Investigation #2

Step 1 Take the scalene acute triangle you constructed in the previous investigation and label it ABC, as shown below. Do not worry if your triangle is a different shape.

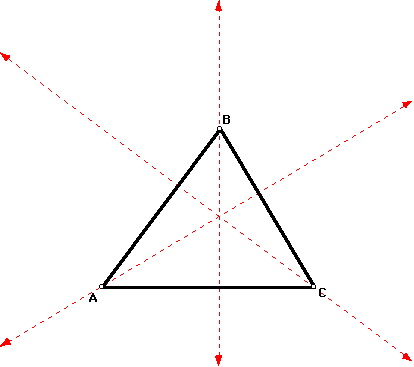
Step 2 Label the three angle bisectors AF, BD, and CE. Label the incenter I.

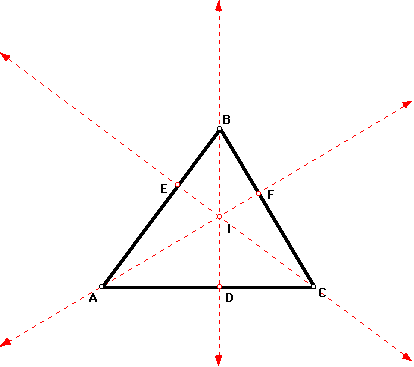
Step 3 Use your compass to answer the following questions: Is the incenter the same distance from the vertices? From the three sides? Take a look at how the incenter divides each bisector into two parts. Is the incenter the midpoint of each bisector?
Step 4 The incenter is not the same distance from the vertices, but it is the same distance from the three sides. The incenter is not the midpoint of each bisector.

Student Activity

Return