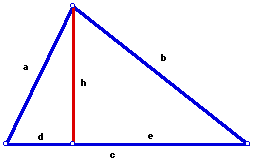

As in the above figure, given a triangle, let the three sides have lengths a, b, and c. Construct the altitude to side c, and let that altitude have length h. Let the distance from the foot of the altiude to the other endpoint of side a be d, and let the distance from the foot of the altitude to the other endpoint of side b be e.
By segment addition, it can be stated that c = d + e. Using the resulting right triangles and the Pythagorean Theorem, it can be stated that d2 + h2 = a2 and e2 + h2 = b2.
By the subtraction property of equality, d2 + h2 - (e2 + h2) = a2 - b2. It follows that d2 - e2 = a2 - b2. Using the division property of equality, since c = d + e, then (d2 - e2)/ (d + e) = (a2 - b2)/ c, which implies that d - e = (a2 - b2)/ c. Using the addition property of equality and c = d + e gives d - e + (d + e)= [(a2 - b2)/ c] + c. Then 2d = (a2 - b2 + c2)/ c. Solving for d gives d = (a2 - b2 + c2)/ 2c.
Using the traditional formula to find the area of a triangle, the given triangle has area A = hc/ 2. Since d2 + h2 = a2, then h = (a2 - d2)1/2. After substituting into the area formula, A = (1/ 2)*c*(a2 - d2)1/2 = (1/ 2)*(a2c2 - d2c2)1/2 = (1/ 2)*[(ac)2 - (dc)2]1/2. Plugging in the above value for d gives A = (1/ 2)*[(ac)2 - (((a2 - b2 + c2)/ 2c)*c)2]1/2 = (1/ 2)*[(ac)2 - ((a2 - b2 + c2)/ 2)2]1/2.
The above equation is equivalent to the equation A = (1/ 2)*[(4(ac)2 - (a2 - b2 + c2)2)/ 4]1/2. Factoring out 1/ 4 gives A = (1/ 2)*(1/ 2)*[(2ac)2 - (a2 - b2 + c2)2]1/2. So it can be stated that 4A = [(2ac)2 - (a2 - b2 + c2)2]1/2; squaring both sides gives 16A2 = (2ac)2 - (a2 - b2 + c2)2.
Factoring the right side of the equation gives 16A2 = [2ac + (a2 - b2 + c2)]*[2ac - (a2 - b2 + c2)]. After some regrouping, 16A2 = [(a2 + 2ac + c2) - b2]*[b2 - (a2 - 2ac + c2)]. Factoring again, 16A2 = [(a + c)2 - b2]*[b2 - (a - c)2]. Finally, factoring once more gives 16A2 = [(a + c) + b]*[(a + c) - b]*[b + (a - c)]*[b - (a - c)] = (a + b + c)(a - b + c)(a + b - c)(-a + b + c).
Since the semiperimeter of the above triangle is defined as s = (a + b + c)/ 2, it follows that 2s = a + b + c, and so 2s - a = b + c. Adding -a to both sides of the equation gives 2s - 2a = -a + b + c. Therefore, 2(s - a) = -a + b + c. Similar algebra steps give 2(s - b) = (a - b + c) and 2(s - c) = (a + b - c).
If follows by substitution that 16A2 = 2s*[2(s - b)]*[2(s - c)]*[2(s - a)]. A little rearranging gives 16A2 = 16s(s - a)(s - b)(s - c), which implies A2 = s(s - a)(s - b)(s - c). Thus, A = [s(s - a)(s - b)(s - c)]1/2, which was to be proved. QED.