I. A brief history of Heron of Alexandria
II. Heron's Formula, including a GSP sketch to test
III. Three proofs of Heron's Formula: one algebraic, one geometric, and one trigonometric
IV. Related topics:
A. Brahmagupta's Generalization, including a GSP sketch to test and a proof
B. An extension of Brahmagupta's Generalization, including a GSP sketch to test
C. The Pythagorean Theorem, including a proof using Heron's Formula
V. Resources
Not much is known about the man named Heron of Alexandria. Even his name is not definite; he has been called Heron and Hero. No one knows exactly when he lived, though it is commonly believed that he lived sometime between 150 B.C. and 250 A.D. Heron did live in the great scholarly city of Alexandria, Egypt, where many Greek mathematicians and scientists studied. Yet it is not known whether he was a Greek or actually an Egyptian with Greek training. What is sure, though, is that Heron of Alexandria was a brilliant man who gave the modern world much insight into the mathematical and physical sciences.
Heron wrote so many works on mathematical and physical subjects that "it is customary to described him as an encyclopedic writer in these fields" (Eves, p. 178). Most of these works can be divided into two categories: geometric and mechanical. While approximately fourteen of his treatises have been uncovered, there are references to other lost works.
One of Heron's treatises, called Pneumatica, describes almost one hundred machines and toys, including a fire engine, a wind organ, and a device for opening temple doors by a fire on the altar. His Dioptra consists of engineering applications of an ancient type of surveyor's transit. The work Catoptrica deals with properties and constructions of mirrors.
Perhaps Heron's greatest contribution to the mathematical world was his work called Metrica, which was written in three books. It was mainly of geometric nature, dealing with area and volume mensuration of various polygons and solids. It investigated properties of regular polygons, circles, and conic sections. In this work Heron also gave a method of finding the approximation of the square root of a non-square integer; this method is used by many computers today.
Finally, Metrica contains Heron's proof of the formula used to find the area of a triangle given the lengths of the three sides. Most scholars believe the proposition should actually be attributed to Archimedes. But the formula was given Heron's name, and it is by the term Heron's Formula that the proposition is now widely known.
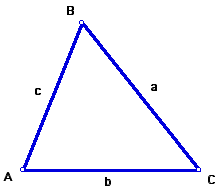
Most schoolchildren know the traditional formula used to find the area of a triangle: A = (1/ 2)*b*h. Obviously, to find the area of a triangle using this formula, one must know the length of a side of the triangle (the base, b) and the length of the altitude to that side (the height, h).
On the other hand, Heron's Formula can be used to find the area of a triangle when one knows the lengths of the three sides. Note that it is not necessary to know a height in order to use this formula.
Heron's Formula states:
Given the lengths a, b, and c of the three sides of a triangle...

...and after finding the semiperimeter, s, of the triangle,...
...the area of the triangle can be found using this formula:
Click here for a Geometer's SketchPad file to manipulate and to relate the traditional area formula to Heron's Formula.
There are many proofs of Heron's Formula. Most can be categorized as algebraic, geometric, or trigonometric. The following list includes a presentation of one proof of each of these types.
Click here to see an algebraic proof of Heron's Formula.
Click here to see a geometric proof of Heron's Formula. This proof is based on Heron's proof of the formula in Metrica.
Click here to see a trigonometric proof of Heron's Formula.
Brahmagupta was a Hindu mathematician who lived in India during the seventh century A.D. He wrote Brahma-sphuta-sidd'hanta, which was mainly a work on astronomy, but two of its chapters dealt with mathematics. Included in this work was a formula that can be used to find the area of a cyclic quadrilateral when given the lengths of the four sides. The formula is often called Brahmagupta's Generalization, as opposed to Brahmagupta's Formula, because later commentators assumed it was a formula to be used to find the area of any quadrilateral. Because they failed to see the limitation of the formula, the critics found that it did not work in all cases.
Given a quadrilateral inscribed in a circle, with sides of length a, b, c, and d,...
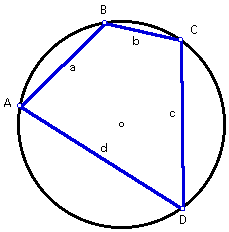
...and after finding the semiperimeter, s, of the quadrilateral,...
...the area of the quadrilateral can be found using this formula:
***Note that when the distance d equals 0, the cyclic quadrilateral becomes a triangle. Brahmagupta's Generalization then reduces to Heron's Formula.
Click here for a Geometer's SketchPad file to test Brahmagupta's Generalization.
Click here to see a proof of Brahmagupta's Generalization.
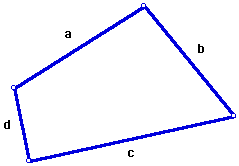
Because Brahmagupta's Generalization works only for cyclic quadrilaterals, it is interesting to note that an extension of his formula can be used to find the area of any quadrilateral.
Given a quadrilateral with sides of length a, b, c, and d,...
...let the measure of the angle between sides a and d be A, and the measure of the angle between sides b and c be B.
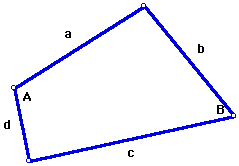
After finding the semiperimeter, s, of the quadrilateral,...
...the area of the quadrilateral can be found using this formula:
***Note that when the distance d equals 0, the quadrilateral becomes a triangle. This extension of Brahmagupta's Generalization then reduces to Heron's Formula.
Click here for a Geometer's SketchPad file to test this extension of Brahmagupta's Generalization.
There are many, many ways to prove the Pythagorean Theorem. One way is to use Heron's Formula.
Given a right triangle with legs of length a and b and hypotenuse of length c,...
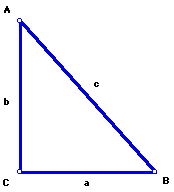
...the following relationship can be stated:
Click here to see a proof of the Pythagorean Theorem using Heron's Formula.
Coxeter, H.S.M. and S.L. Greitzer. Geometry Revisited. Random House, Inc., New York City, 1967.
Eves, Howard. An Introduction to the History of Mathematics, 6th ed. Saunders College Publishing, Orlando, 1990.
Kevin Brown's MathPages: http://www.seanet.com/~ksbrown/kmath196.htm
Cut-the-Knot: http://www.cut-the-knot.com/pythagoras/herons.html
Dr. Jim Wilson's problem solving course: http://jwilson.coe.uga.edu/emt725/Heron/Trig.Heron.html