MATH 7200 : Foundations of Geometry I

University of Georgia, Fall 2000

Dr. McCrory, Instructor

A Trigonometric Proof of Heron's Formula

by Shannon Umberger

Note: This proof was adapted from a proof on Dr. Jim Wilson's website (Department of Mathematics Education, College of Education, University of Georgia).

http://jwilson.coe.uga.edu/emt725/Heron/Trig.Heron.html

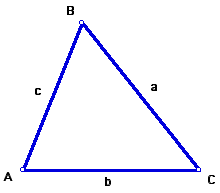
Given a triangle with sides of lengths a, b, and c. Trigonometry gives an area formula that states A = (1/ 2)absinC, where C is the angle opposite side c.

Using the Law of Cosines, c2 = a2 + b2 - 2abcosC. Solving for cosC gives cosC = (a2 + b2 - c2)/ 2ab. Rearrange the Pythagorean identity (sinC)2 + (cosC)2 = 1 to state sinC = [1 - (cosC)2]1/2. By substitution, sinC = [1 - ((a2 + b2 - c2)/ 2ab)2]1/2.

Factoring gives sinC = [(1 + (a2 + b2 - c2)/ 2ab)*(1 - (a2 + b2 - c2)/ 2ab)]1/2. It follows that sinC = [((2ab + a2 + b2 - c2)/ 2ab)*((2ab - a2 - b2 + c2)/ 2ab)]1/2. Factoring out the denominator gives sinC = (1/ 2ab)*[(2ab + a2 + b2 - c2)(2ab - a2 - b2 + c2)]1/2.

After some regrouping, sinC = (1/ 2ab)*[((a2 + 2ab + b2) - c2)(c2 - (a2 - 2ab + b2))]1/2. Factoring gives sinC = (1/ 2ab)*[((a + b)2 - c2)(c2 - (a - b)2)]1/2. After factoring once more, sinC = (1/ 2ab)*[((a + b) + c)((a + b) - c)(c + (a - b))(c - (a - b))]1/2. With some rearranging, sinC = (1/ 2ab)*[(a + b + c)(a + b - c)(a - b + c)(-a + b + c)]1/2.

Since the semiperimeter of the above triangle is defined as s = (a + b + c)/ 2, it follows that 2s = a + b + c, and so 2s - a = b + c. Adding -a to both sides of the equation gives 2s - 2a = -a + b + c. Therefore, 2(s - a) = -a + b + c. Similar algebra steps give 2(s - b) = (a - b + c) and 2(s - c) = (a + b - c).

If follows by substitution that sinC = (1/ 2ab)*[2s*[2(s - c)]*[2(s - b)]*[2(s - a)]]1/2. With some rearranging, sinC = (1/ 2ab)*[16s(s - a)(s - b)(s - c)]1/2 = (1/ 2ab)*4*[s(s - a)(s - b)(s - c)]1/2 = (2/ ab)*[s(s - a)(s - b)(s - c)]1/2.

Now, substitute the value of sinC into the area formula A = (1/ 2)absinC. So, A = (1/ 2)*ab*(2/ ab)*[s(s - a)(s - b)(s - c)]1/2. Thus, A = [s(s - a)(s - b)(s - c)]1/2, which was to be proved. QED.

Return to Heron's Formula main page