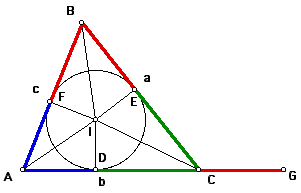
Given triangle ABC, let the length of segment BC be a, the length of segment AC be b, and the length of segment AB be c.
Note the perimeter, p, of triangle ABC = a + b + c. Half of the perimeter is called the semiperimeter, s, and so for triangle ABC, s = (a + b + c)/ 2.

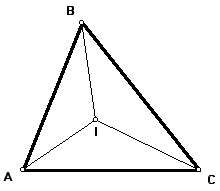
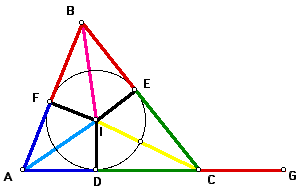
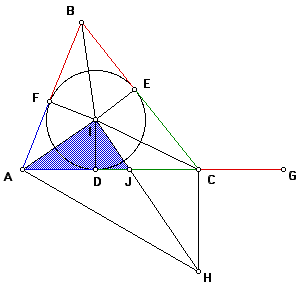
Let the point of intersection of the angles bisectors of angles A, B, and C be called point I. Construct segments AI, BI, and CI.
Next, let the point of intersection of the perpendicular to side AC through point I be called point D, the point of intersection of the perpendicular line to side BC through point I be called point E, and the point of intersection of the perpendicular line to side AB through point I be called point F.
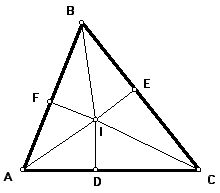
By definition, point I is called the incenter of triangle ABC. The circle with point I as the center and that passes through points D, E, and F is called the incircle of triangle ABC.
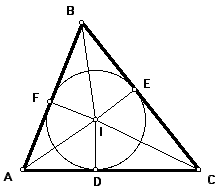
Now, since segment IB is the angle bisector of angle B, then angles IBF and IBE are equal. Since angles IFB and IEB are right by construction, then they are equal, and thus angles BIF and BIE are equal (since all angles of a triangle sum to 180 degrees). Note that segments IF and IE are equal since both are radii of the same circle. Therefore, triangles BIF and BIE (in red) are congruent by SAS.
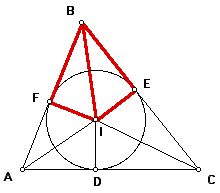
Similarly, triangles CID and CIE (in green) are congruent by SAS.
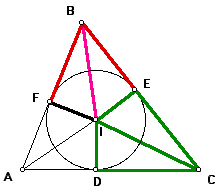
Also similarly, triangles AIF and AID (in blue) are congruent by SAS.
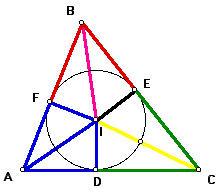
Because corresponding sides of congruent triangles are congruent, it follows that segments BF and BE (in red) are equal, segments CD and CE (in green) are equal, and segments AD and AF (in blue) are equal.
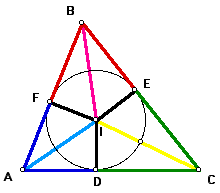
By using the formula that states the area of a triangle equals one-half the base times the height, the area of triangle AIB = (1/ 2)*AB*IF,...
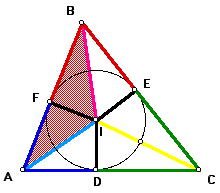
...the area of triangle BIC = (1/ 2)*BC*IE,...
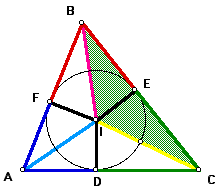
...and the area of triangle AIC = (1/ 2)*AC*ID.
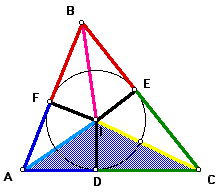
Therefore, the area of triangle ABC is the sum of the areas of triangles AIB, BIC, and AIC.
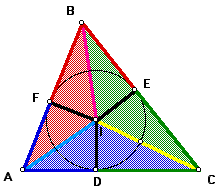
By substitution, the area of triangle ABC = (1/ 2)*AB*IF + (1/ 2)*BC*IE + (1/ 2)*AC*ID. Since segments IF, IE, and ID are equal (they are all radii of the same circle), it follows with a little algebra that the area of triangle ABC = (1/ 2)*ID*(AB + BC + AC). But AB + BC + AC = a + b + c, and so this sum is really the perimeter of triangle ABC; therefore, the area of triangle ABC = (1/ 2)*ID*p. Since (1/ 2)*p = s, the semiperimeter of triangle ABC, then the area of triangle ABC = ID*s.
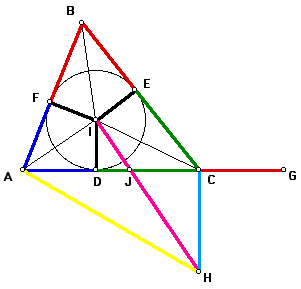
Now, construct point G such that G lies on the same line as segment AC, and segment CG equals segment BE. Remember p = a + b + c = AB + BC + AC, and so by segment addition and substitution, p = (BE + CE) + (CD + AD) + (AF + BF) = (BF + BE) + (CE + CD) + (AD + AF). Furthermore, by substitution, p = 2*BE + 2*CD + 2*AD = 2(BE + CD + AD). Again, by substitution, p = 2(CG + CD + AD). But, AG = AD + DC + CG by segment addition, and so by substitution, p = 2*AG. Therefore, s = AG.
Thus, by substitution, the area of triangle ABC = ID*AG.
Construct a line perpendicular to segment AI through point I (in pink) and a line perpendicular to segment AG through point C (in light blue). Let the point of intersection of these two lines be called point H. Let the point of intersection of segment IH and segment AG be called point J. Construct segment AH (in yellow).
Since angles AIH and ACH are right (by construction), then triangles AIH and ACH are right. Note the triangles share a common hypotenuse, segment AH. It follows that these triangles are inscribed in a common circle with segment AH as the diameter of the circle.
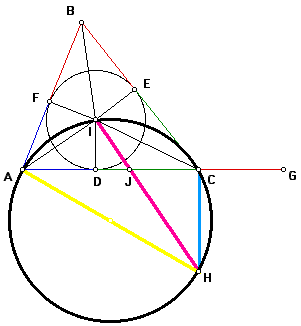
This fact means that quadrilateral AICH is cyclic, and so opposite angles AIC and AHC are supplementary.
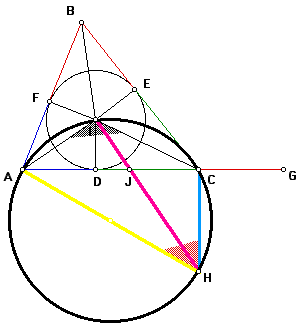
Since the sum of the angles at point I is 360 degrees, by angle addition, (angle BIF + angle BIE) + (angle CIE + angle CID) + (angle AID + angle AIF) = 360 degrees. By substitution, 2*(angle BIE) + 2*(angle CID) + 2*(angle AID) = 360 degrees, and so angle BIE + angle CID + angle AID = 180 degrees. But angle CID + angle AID = angle AIC by angle addition, thus angle BIE + angle AIC = 180 degrees, and so angles BIE and AIC are supplementary.
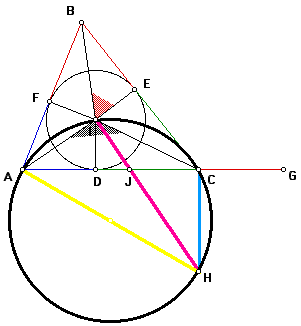
Since angles BIE and AHC are supplementary to the same angle, it follows that angle BIE = angle AHC.
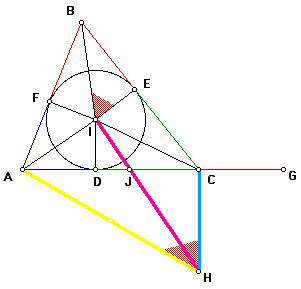
Because angles BIE and AHC are equal, and angles BEI and ACH are equal (both are right by construction), then triangles BIE and AHC are similar by AA similarity.
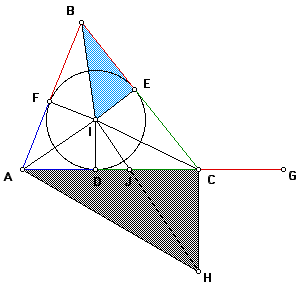
By substitution, AC/CG = AC/BE. Then, by the definition of similar triangles, AC/BE = HC/IE.
Now, because angles IJD and HJC are vertical angles, they are equal. Also, angles IDJ and HCJ are equal (both are right by construction). Therefore, triangles IJD and HJC are similar by AA similarity.
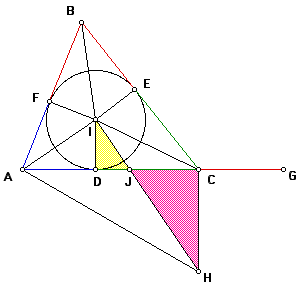
By substitution, HC/IE = HC/ID. Then, by the definition of similar triangles, HC/ID = CJ/DJ.
Thus, by transitivity, AC/CG = CJ/DJ.
The next few steps of the proof require a few algebra tricks.
Since AC/CG = CJ/DJ, then AC/CG + 1 = CJ/DJ + 1.
So AC/CG + CG/CG = CJ/DJ + DJ/DJ.
This implies that (AC + CG)/CG = (CJ + DJ)/DJ.
But by segment addition, AC + CG = AG, and CJ + DJ = CD.
Therefore, by substitution, AG/CG = CD/DJ.
Well, then, AG/CG * 1 = CD/DJ * 1.
So AG/CG * AG/AG = CD/DJ * AD/AD.
Then AG2/CG*AG = CD*AD/DJ*AD.
Now, since triangle AIJ is right (by construction), and D is a point on the hypotenuse, then DJ*AD = ID2 (by the geometric mean).
So, by substitution, AG2/CG*AG = CD*AD/ID2.
By cross multiplication, AG2*ID2 = CG*AG*CD*AD.
It follows that AG*ID = [CG*AG*CD*AD]1/ 2.
But, the area of triangle ABC = AG*ID.
Thus, by transitivity, the area of triangle ABC = [CG*AG*CD*AD]1/ 2.
Finally, remember that segment AG = s.
Note that segment CG = AG - AC by segment addition, and so CG = s - b by substitution.
Also note that segment CD = AG - (AD + CG) by segment addition. So CD = AG - (AF + BF) by substitution, and so CD = s - c by substitution.
And note that segment AD = AG - (CD + CG) by segment addition. So AD = AG - (CE + BE) by substitution, and so AD = s - a by substitution.
Therefore, by substitution, the area of triangle ABC = [s*(s - a)*(s - b)*(s - c)]1/ 2. QED.