Given two circles and a point on one of the circles, construct a circle tangent to the two circles with one point tangency being the designated point.

Here are some examples of the problem. The red circle is the tangent circle to the given two circles. The first three examples are when the one of the given circles is inside the other given one.

The next three examples show the the tangent circle when the two given circles intersect each other.

And, the final three examples show one of the given circles outside the other given circle.

For a dynamic presentation of the tangent circle click on one of the following below:

• Animation of the tangent circle when one of the two given circles is inside the other.
• Animation of the tangent circle when the two given circles intersect each other.
• Animation of the tangent circle when one of the two given circles is outside the other.

We need to also consider that the tangent circle could be drawn like the figures below.

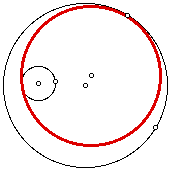
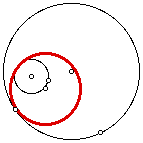
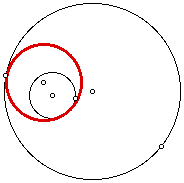
For a dynamic presentation of the tangent circle in the above figures click here.

Now, let's take a look at some interesting discoveries that I found while playing around with the locus of the center of the tangent circle.

First, if the center of the two circles coincide, then the locus of the center of the tangent circle to these two will be a circle. See drawing below.

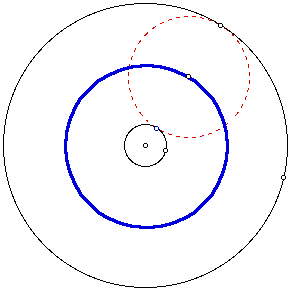
For an animation of the figure above click here.

Next, I noticed as the smaller circle (while remaining inside the larger cirlce) moved away from the center of the larger circle, the locus of the center of the tangent circle began to take the shape of an ellipse. See the drawing below.

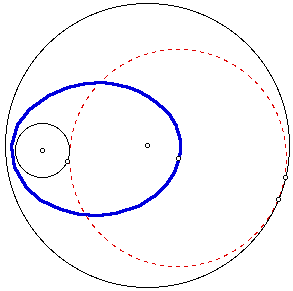
For an animation of the figure above click here.

As the smaller circle continues to move away from the center of the larger circle, we see the locus of the center of the tangent circle getting more elongated.

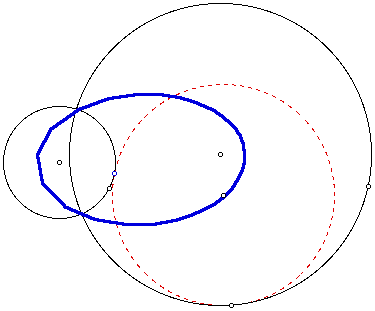
For an animation of the figure above click here.

Finally, when the distance of the two centers is greater than the sum of the two radii the locus of the center of the tangent circle appears to take the shape of a hyperbola.

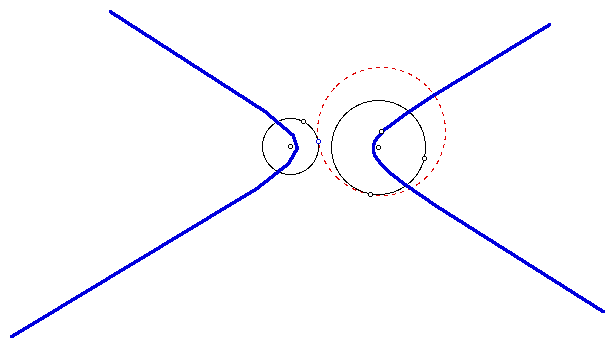
For an animation of the figure above click here.

Let's also take a look a the trace of the centers of both tangent circle. Click here to view this animation.

Return (click this one to return to Circles Lesson 7 page)