

A tangent to a circle is a line in the plane of the circle that meets the circle in exactly one point, called the point of tangency.
Tangent circles are two circles that are tangent to the same line at the same point. They can be internally tangent or externally tangent.
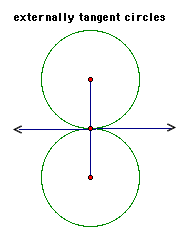
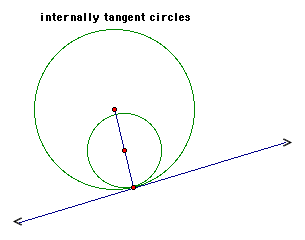
Click here
to explore tangent circles even further.
Lesson Investigation 1:
Use a compass to draw a circle. Label the center P. Use a straightedge to draw a line that appears to be tangent to circle P. Label the point of tangency Q. Draw the radius segment PQ. Use a protractor to measure the angles made by the radius and the tangent. What can you conclude? ANSWER
Do the same investigation using Geometer's sketchpad.
The investigation above leads to the following theorems:
If a line is tangent to a circle, then it is perpendicular to the radius drawn to the point of tangency.
In a plane, if a line is perpendicular to a radius of a circle at its endpoint on the circle, then the line is tangent to the circle.
Lesson Investigation 2:
Use a compass to draw a large circle. Label the center of the circle as P. Choose a point in the circle's exterior and label it S. Draw to lines that appear to be tangent to circle P. Label the points of tangency as R and T. Use your compass to compare the lengths of segments RS and ST (segments RS and ST are called tangent segments). What can you conclude?
Now use Geometer's sketchpad
to do the same investigation.
The following theorem follows as a result of investigation 2:
If two segments from the same
exterior point are tangent to a circle, then they are congruent.
Click here for exercises for lesson 3.