There are several cases to explore when investigating this problem.  Is one of the circles contained inside the other, do the two circles intersect, or are the two circles disjoint?  I will begin my exploration when one of the circles is completely contained within the larger one.

To see a step-by-step guide on how to construct the common tangent circle to the given two circles, click here.

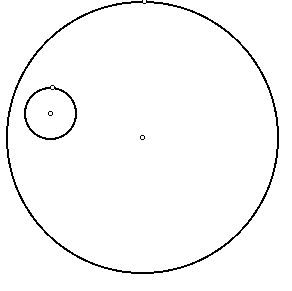
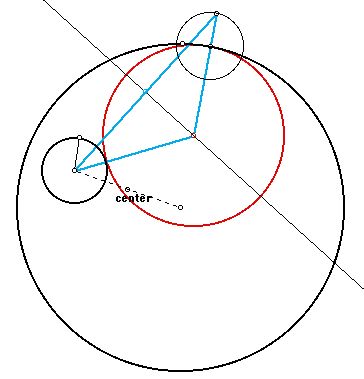
In constructing the common tangent circle to the two given circles, we can form an isosceles triangle (in light blue.)  Note that the common tangent circle is in red.

The center of the desired tangent circle lies along the perpendicular bisector of the base of the isosceles triangle.  The triangle is isosceles since two of the sides are both the sum of the radius of the smaller circle and the radius of the tangent circle.

The center of the tangent circle forms an ellipse as the designated point moves along the larger circle.
Click here to see an animation of this discovery.  Want a proof?  Click here.
In some cases, the locus of the center of the common tangent circle forms a hyperbola.  Click here for a proof.

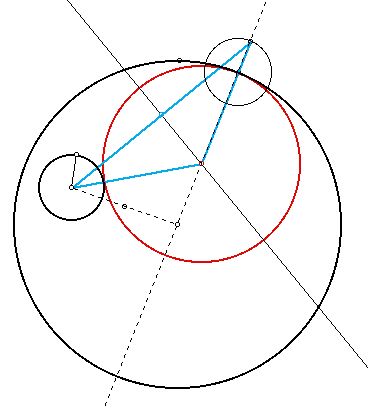
Radius
To investigate the radius of this new circle, compare the locus of the midpoint and the locus of center of the common tangent circle.

The radius of the light blue circle seems to equal the length of the distance from the center of the red ellipse to the point of intersection of the ellipse and it's major axis.  The major axis is the dashed line connecting the centers of the two original circles.

We can construct the radius and thus the circle formed by the locus of the midpoint.  To do this, first construct an equilateral triangle, with one side given by the segment connecting the centers of the original circles.  For convenience, call this segment j.  Next, find the altitude from segment j to the opposite vertex. The altitude forms the radius of the circle!!  See the illustration below, focusing on the highlighted yellow equilateral triangle.

So, we have discovered that the midpoint of the base segment of the isosceles triangle forms a path of a circle as the designated point on one of the original circles moves along the circle.  The center of this new circle is at the midpoint of the segment connecting the two original centers.  The radius can be illustrated with the altitude of an equilateral triangle formed with the segment connecting the centers of the original two circles.

To see more cases, click here.

Throughout all cases except one, the locus of the midpoint is a circle.  The center is located at the midpoint of the segment connecting the two centers of the original circles.  (See the case of the intersecting circles for an exception.)  The radius does always seem to be the length of the distance from the center of the formed ellipse to the point of intersection of the ellipse and its major axis, i.e., half of the major axis.  In some cases, the locus of the center of the common tangent circle forms a hyperbola, in which case, the traced circle of the midpoint of the base of the isoscelses triangle is tangent to the hyperbola.
 

Exception!
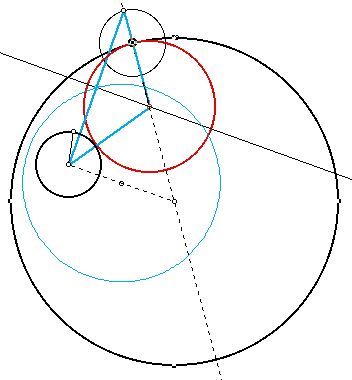
As you search through the cases where the midpoint of the triangle is traced, the path does form a circle.  There is an exception, however!  When the two original circles intersect, the trace of one common tangent forms a circle, but the other forms a hyperbola.  When the locus of the center of the common tangent forms a hyperbola, the midpoint of the segment of the triangle no longer forms a circle.  Take a look below at the unusual locus of the midpoint, shown in light blue.  Note that the hyperbola is in dark blue.