DAY 1 - RATIOS IN A RIGHT TRIANGLE - Mary H. Bruce - EMAT 6690

Objective:  Students will calculate ratios within a right triangle and use these ratios to find missing lengths and angle measures.

Given a right triangle, students are reminded of the Pythagorean Theorem.  CLICK here for an illustration and confirmation that the theorem is satisfied for any right triangle no matter what the sides or acute angle measures are.

Thus, given any two sides of a right triangle, students should be able to find the missing third side by using the Pythagorean Theorem.

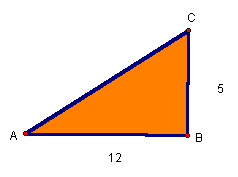
Example 1

    Find the length of segment AC given that angle B is a right angle.

Example 2

    Find the length of segment BC given that angle B is a right angle.

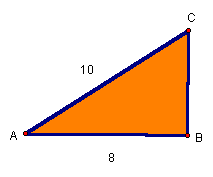
Example 3

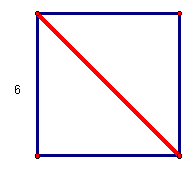
    Find the length of the diagonal of the square.

Students are then asked to use GSP to construct two triangles and examine ratios as shown.  CLICK here for an illustration.

Based on previous knowledge of similarity, students should be able to explain why the side ratios of the right triangle remain the same no matter what the size.

Next, students will be taught the names and formulas of the trigonometric ratios of a right triangle.

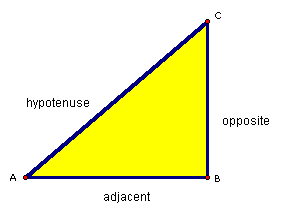
sin A = opposite/hypotenuse

cos A = adjacent/hypotenuse

tan A = opposite/adjacent

Example 4

    Given right triangle ABC, find the missing side.

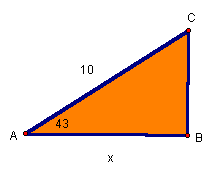
Students should realize since they do not know two sides of the right triangle they must use trigonometry to solve for the missing length.

Example 5

    Given right triangle ABC, find the missing angle.

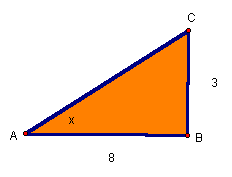
Since the angle is unknown, it is necessary to use an inverse trig function to solve.

Example 6

    Given right triangle ABC, compute sin A, cos A, tan A and sin C, cos C, tan C.  Note any relationships you see.  Explain.

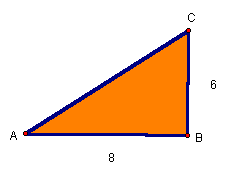
Can the sine and cosine ratios ever be larger than 1?  Can the tangent ratio ever be larger than 1?  Explain.

RETURN to Instructional Unit Outline