DAY 2 - Degrees and Radians/Coterminal and Reference Angles - Mary H. Bruce - EMAT 6690
Objective: Students will be able to locate the terminal side of an angle in degrees or radians, change from degrees to radians or vice versa and name coterminal and reference angles.
Students come into a trigonometry course generally with a geometric background that assumes perhaps that angles might not be larger than 180˚. Have students visualize a ballerina spinning around in continuous revolutions. What degree of rotation did she turn? Suppose she stops and goes in the opposite direction. Students begin to discern that their previous notion of angles from geometry is about to change. Let an angle be in initial position when both initial and terminal sides are on the positive x-axis. CLICK here for an illustration of the rotation. Knowing that a full circle measures 360˚ one can understand that by adding or subtracting multiples of 360, an angle will have a terminal side at the same position thus called coterminal angles.
Example 1: Draw the terminal sides of angles of 240˚, 315˚, 450˚ and -150˚ Find another positive and negative coterminal angle for each.
No matter what quadrant your angle falls in, there will always be an angle formed by the terminal side and the x-axis. This is called a reference angle. CLICK here for an illustration.
Notice that a reference angle will always be between 0˚and 90˚inclusively. If your angle Θ falls in the first quadrant then Θ=Θref. If your angle falls in the second quadrant then Θref = 180 - Θ. If your angle falls in the third quadrant then Θref = Θ - 180, and if your angle falls in the fourth quadrant then Θref = 360 - Θ. These formulas assume your angle or coterminal angle is between 0˚and 360˚.
Example 2: Given the measures of Θ from example 1, find reference angles for each.
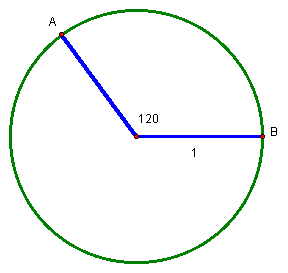
Finally for every angle degree measure there is a corresponding radian measure. Review arc length from geometry. Given a central angle, the intercepted arc is a corresponding portion of the circumference of the circle.

Arc length = arc measure/360 * 2Πr so in the case of a unit circle of radius 1, we would get the arc length to be 120/360 * 2Π which would reduce to 2Π/3. Thus, the radian measure or arc length for a 120˚angle of a unit circle would be 2Π/3. In short, one can always convert from degrees to radians by multiplying by Π/180 or from radians to degrees by multiplying by 180/Π given a unit circle.
Example 3: Convert the following degrees to radians - 150˚, 270˚, 60˚, -120˚.
RETURN to Instructional Unit Outline