DAY 3 - The Unit Circle - Mary H. Bruce - EMAT 6690

Objective:  Students will be able to generate degrees, radians and coordinates of the unit circle and find exact values of trig functions using this knowledge.

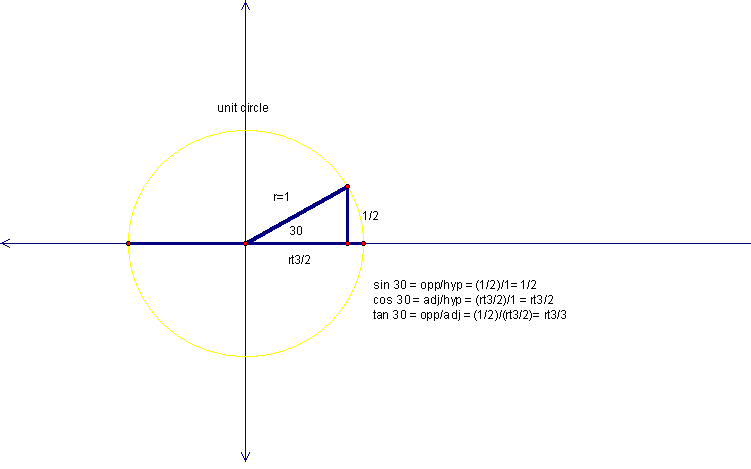
Recall from day 2 that radian measure is simply arc length.  A unit circle is defined to be a circle of radius 1.  Thus from circumference = 2Πr one can understand that 2Π is the radian measure that corresponds with one full revolution around the circle.  Using this knowledge and that gained from the previous days' discussions, the radian measures and their corresponding degrees around the unit circle can be calculated.  If the circle is a unit circle then the radius must be a length of 1, and dropping a perpendicular from a point on the unit circle to the x-axis creates a right triangle as discussed day 1.  The radius of 1 equates to the hypotenuse of the right triangle formed having a length of 1.  Using previous knowledge of 30-60-90 and 45-45-90 triangles from geometry, coordinates around the unit circle can be derived.

The complete unit circle:

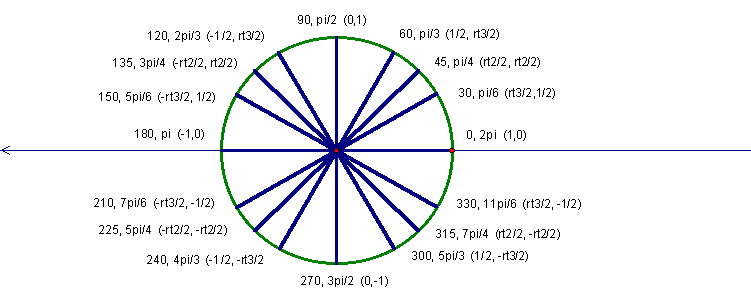
Notice that the ordered pairs are based on the reference angles that go with each angle and signs of the coordinates correspond to the particular quadrant that contains the terminal side.  Click here for a GSP animation.

Based on the trigonometric ratios from day 1, with a hypotenuse of 1, we can see that the x-coordinate is simply the cosine of Θ (actually rcosΘ), and the y-coordinate is the sine of Θ (actually rsinΘ).  The tangent ratio could be calculated by dividing the y-coordinate (opposite side) by the x-coordinate (adjacent side).  Thus, tanΘ = sinΘ/cosΘ.

Example 1:  Find exact values of the following:

                        sin 135˚

                        cos 240˚

                   tan 330˚

                        cos 4Π/3

                        tan 11Π/6

                        sin Π/2

RETURN to Instructional Unit Outline