DAY 6 - Tangent and Reciprocal Graphs - Mary H. Bruce - EMAT 6690

Objective:  Students will be able to graph y = tan x, y = cot x,  y = csc x and y = sec x

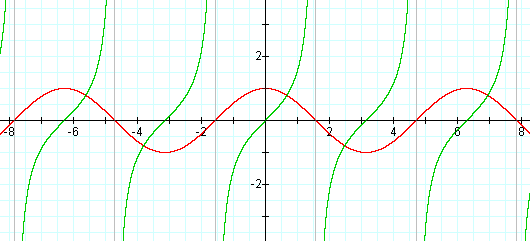
Based on previous discussion we realize that tan x = sin x/cos x.  Due to the rational nature of this function we can guess that the domain will be restricted.  Since cos x  is in the denominator we would expect vertical asymptotes everywhere that cos x = 0.  This would correspond with the x-intercepts of the y = cos x graph.  CLICK here for a GSP animation of the y = tan x graph as developed from the unit circle.  Using Nucalc, we can graph y = cos x and y = tan x simultaneously to see the relationship between the intercepts and the asymptotes.

 One should notice that the period of the tangent graph is half the length of the cosine graph.  Since tangent is simply the same as slope (y/x) it only takes an interval of Π for the pattern to repeat itself.

The reciprocal trig functions are as follows:  csc x = 1/sin x,   sec x = 1/cos x,   cot x = 1/tan x.  One should deduce that the x-intercepts of the original graphs will now become vertical asymptotes, maximums will now become minimums and vice versa.

Using a GSP animation the inverse relationship becomes very evident with the opposite motion involved.  CLICK here for an animation of  y = sin x and y = csc x.  Or a stationary examination using Nucalc:

CLICK here for a GSP animation of y = cos x and y = sec x.

CLICK here for a GSP animation of y = tan x and y = cot x.

RETURN to Instructional Unit Outline