DAY 7 - Applications - Mary H. Bruce - EMAT 6690

Objective:  Students will apply the concepts learned in this unit to problem-solving situations.

In right triangle word problems, students should be familiar with the terms angle of elevation and angle of depression.

The angle of elevation is formed when someone or something is looking out and looking up at an object.  The angle of depression is formed when someone or something is looking out and looking down at an object.

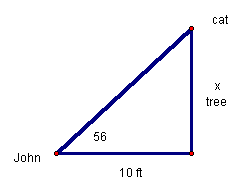
Example 1:  John is looking up at his cat at the top of the tree.  If John is standing 10 feet away from the tree and the angle of elevation is 56˚ how high up is the cat?

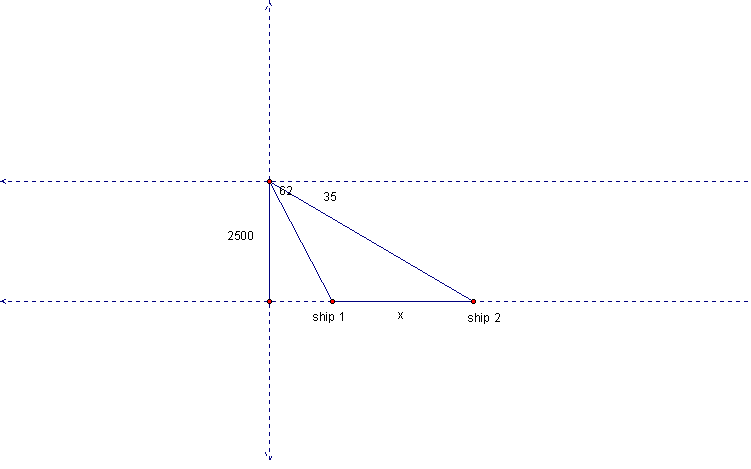
Example 2:  At the top of an observation tower, a coast guard spots two ships at angles of depression of 62˚ and 35˚respectively.  How far apart are the ships if the tower is 2500 feet high?

Example 3:  As you ride a bicycle, the distance between your foot and the pavement varies sinusoidally with the horizontal distance the bicycle has gone.  Suppose that you start with your right foot somewhere between a high point and a low point and push down.  When you have gone 5m, your right foot first reaches its lowest point, 11 cm above the pavement.  The high points are 45 cm above the pavement.  The bicycle moves a horizontal distance of 16.4 m for each complete revolution of the pedals.

    (a)  Sketch the graph.

    (b)  Write an equation for the sinusoid.

    (c)  How high was your right foot when you first started?

Students should look for clues from the problem for amplitude, period, phase shift and vertical translation.  The vertical translation (middle axis of the graph) will always be halfway between the minimum and the maximum.  Thus (11+45)/2 = 28.  The amplitude is the distance from the middle axis to the maximum,  45 - 28 = 17.  The period is the length of one full cycle and is equal to 2Π/|b| so 16.4 = 2Π/ b so b = 5Π/41.  The phase shift is at 5 m and since it is a low point rather than a high point it implies a negative coefficient in front of cosine.  Thus the equation is f(x) = 28 - 17cos5Π/41(x - 5).  To get part c, simply evaluate the function at x = 0.

Example 4:  Lab technicians are studying the behavior of Cristina's gerbil after receiving high doses of medication.  The gerbil starts at the point (1,0) and moves in a circular path around the origin. He moves a distance of 5.41 in a clockwise direction.

    (a)  What is the ordered pair location of the gerbil?

    (b)  Find the angle formed with the gerbil, the origin and the positive x-axis.

    (c)  If a technician then places food at the point (-1,0), how far will Cristina's gerbil have to travel from its current spot to reach the food (assuming the disoriented gerbil turns around and travels counterclockwise in a circular path around the origin)?

Hint:  Think of the relationship between degrees and radians and the unit circle.

RETURN to Instructional Unit Outline