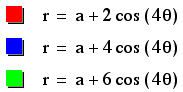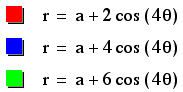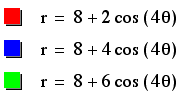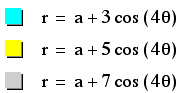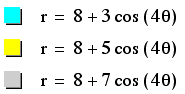Untitled Document

Varying b

Even Variation

For this part of our investigation, we will vary the value of b by even numbers while keeping a and k constant.

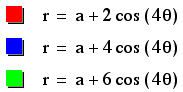
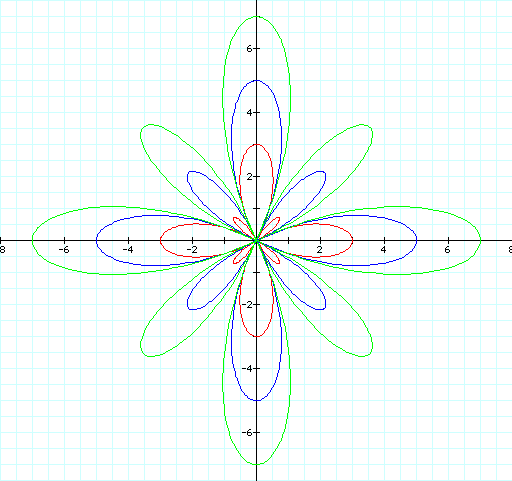Above we see that our rose is symmetrical, but we have doubled the number of petals from k.

This occurs not only when b is less than k, but also when b is greater than k.

We can see that as b increases on the even numbers, the rose petals get larger and larger, yet still stay tight around the origin.

They stay focused on the origin, because we have not varied a, which we saw to govern this characteristic earlier.

What if a is larger than b?

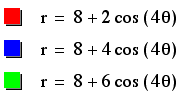
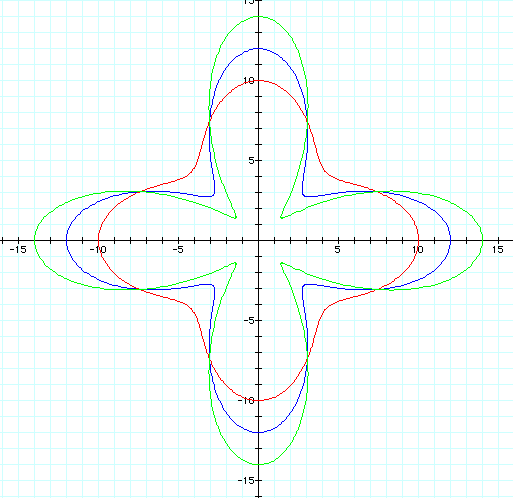Since we have varied a, we see the petals spreading from the origin.

But, why is it back to four petal?

Well, it is just as the investigation of a went. We now have a larger than b, so we get the true number of petals to match k.

Odd Variation

For this part of our investigation, we will vary the value of b by odd numbers while keeping a and k constant.

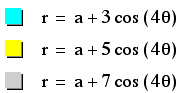
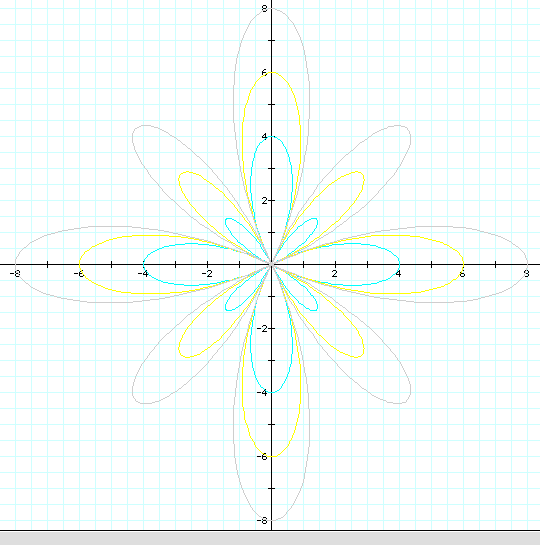Once again, we see the petal enlargement trend as b increases, with our petals being double the value of k.

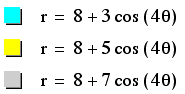
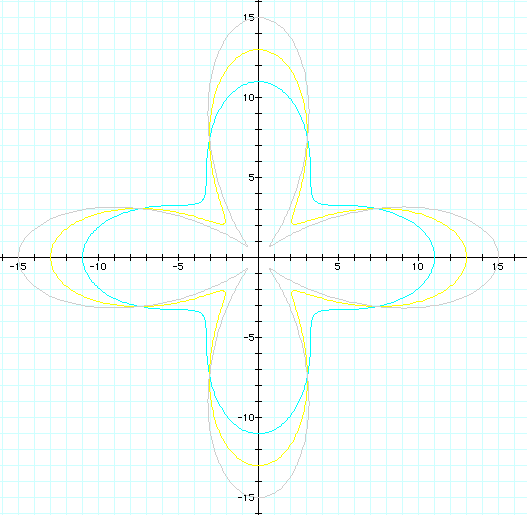The same thing occurs when we hold a to be greater than b, as with the even variation.

We have solved another piece of polar equation puzzle.