

(See problem 15 of Assignment 4.)
The INCENTER (I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides. Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then I must be on the angle bisector of each angle of the triangle.
(See problem 4 of Assignment 4.)
Click here for a GSP script to create the incenter of a given triangle.
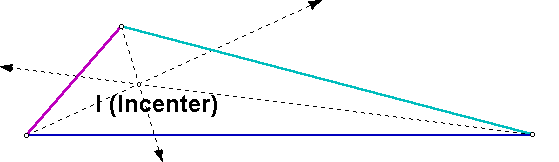
Click here for a GSP sketch of a triangle and its incenter.
Notice that the incenter of the triangle is always inside the triangle, regardless of whether the triangle is acute, right, or obtuse.

The incenter is the center of the incircle of the triangle. In other words, the incenter is the center of the circle that is inscribed in the triangle.
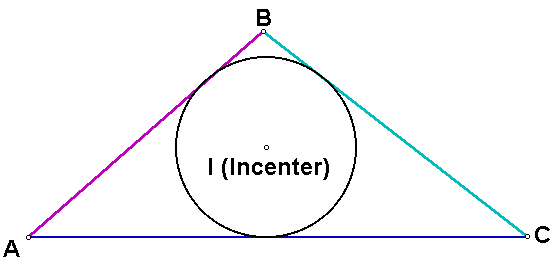
Click here for a GSP sketch of a triangle and its incenter and incircle.
So, there is a name for the intersection of the three angle bisectors of the internal angles of triangle, but how do we know that these three angle bisectors intersect at all?
Click here for a proof of the fact that the three angle bisectors of the internal angles of a triangle are concurrent.