

Now consider the following polar equation:
![]()
Let's first consider the case where k is odd, as in the equations
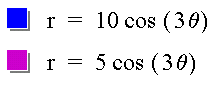
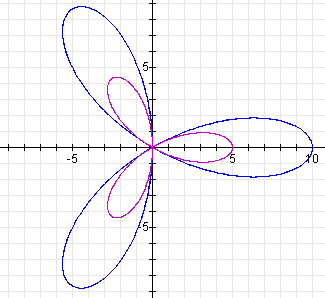
Looking at the graph, we see that k determines the number of leaves, and each leaf is b units long. They are equally spaced around the origin, and the end of one of the leaves is on the positive x-axis.
When b is negative, the graph is rotated ![]() /k
radians from the graph when b is positive:
/k
radians from the graph when b is positive:
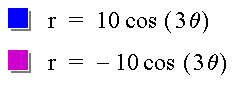
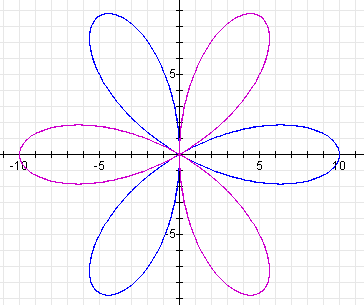
Now let k be even, as in the equations
We see from the graph that the number of leaves is 2k, and each leaf is b units long.
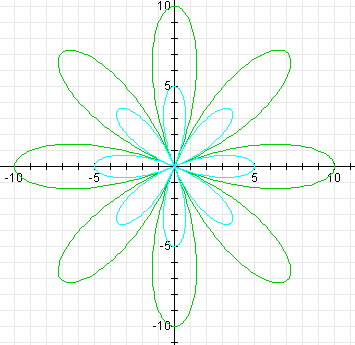
When b is negative, the graph is the same.
Conclusions about the graph of the polar equation
![]()
When k is odd, the rose has k leaves.
When k is even, the rose has 2k leaves.
The leaves are equally spaced about the origin.
The length of each leaf (the distance from the origin to the point farthest from the origin) is | b |.
When k is odd and b is negative, the graph is
rotated ![]() /k radians
from the graph when b is positive.
/k radians
from the graph when b is positive.
When k is even and b is negative, the graph is the same as the graph when b is positive.