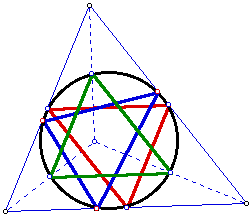
In this assignment we will discuss the nine-point circle, which is a common circumcircle through three special triangles: the medialtriangle, the orthictriangle, and the triangle through the three midpoints of the segments from the orthocenter to the vertices. We will examine each of these triangles individually initially, then we will discuss their relation to the nine-point circle.
Triangle through midpoints of the segments from orthocenter to the vertex
So, we have seen each of our three special triangles, respectively. When all three of these triangles are within the same original traingle we can construct a common circumcircle through the nine vertices. This will be our nine-point triangle. Let's see how this might look:
