My first task is to create the orthocenter H of triangle ABC. Then, once I find that point H, I am asked to find the orthocenters of triangles HBC, HAB, HAC. Then I will draw the circumcircles of each of my triangles. Let's see how this all might look:

The first thing that I noticed is that the orthocenters of the three smalller triangles lie on the vertices of my original triangle ABC. Also, the intersections of the triangles are on the vertices of ABC, for any two circles. However, and more importantly, the three circumcircles of the smaller triangles intersect at the original orthocenter of triangle ABC. Furtermore, all four triangles are congruent. I'm sure that there is a meaningful proof behind this somewhere, but it "avoids" me!

Question?: What would happen if we moved one of our vertices of triangle ABC to where the orthocenter is? Where would the new orthocenter be?

Well, after working with the GSP file on the webpage I noticed that after moving the vertex on top of the orthocenter my new orthocenter will be where the original vertex was. Furthermore, the origial circle lies directly on top of one of my three secondary circles. By the way, this also shows that the triangles are all the same size.

Now, I am asked to construct the nine point circles of the four individual triangles. Let's see how this will look:

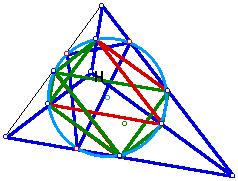
It appears that the four different circles end up one and the same. I can't prove that this is necessarily the case, but this would seem to make sense given what we saw in the last question.

Now, I want to move on to another topic. Given triangle ABC, I need to find the incircle, its three excircles, and its nine point circle. To view a sketch of this Click Here. The main thing we can see here is that our nine-point circle is tangent to the other four circles.

Now, I want to construct any acute triangle ABC and its circumcircle. Then, I will construct the three altitudes AD, BE, and CF, extending each altitude to intersect with the circumcircle.

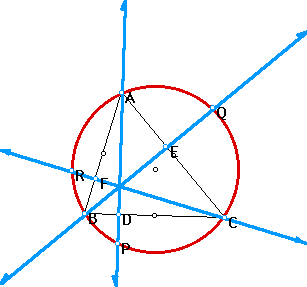
Now, given triangle ABC, construct the orthocenter H. Also, let D, E, and F be the feet of the perpendiculars from A, B, and C, respectively. Let's see how this looks:

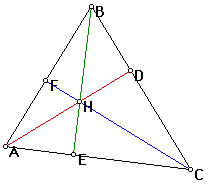
We want to show: HD/AD+HE/BE+HF/CF=1

Well, this proof uses the fact that the orthocemter is two-thirds from one side to the other in a triangle. So we have:

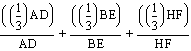
Then, obviously, this reduces to 1/3+1/3+1/3=1

Now, let's prove: AH/AD+BH/BE+CH/CF =2

Well, we will use the same reasoning as before to get:

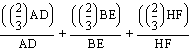
Then, obviuosly, this reduces to 2/3+2/3+2/3 = 6/3 =2

Finally, let's construct triangle ABC, its orthocenter, and the circumcircle for ABH. We will use AB as a "mirror" for triangle ABC. Let's see how this looks:

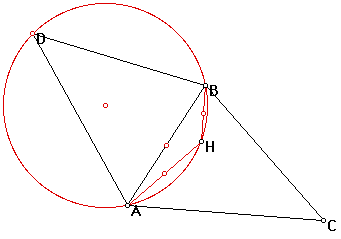
Well, it looks like this gives a pretty good proof of the first problem that we looked at in this assignment. I guess what this shows is that the mirror of point C lies on the circumcircle of ABH. Likewise, the mirror image of point B lies on the circumcircle of AHC. Likewise, the mirror image of point A lies on the circumcircle of BHC. So, I guess what this proves is a way to find the reflection of a triangle across any one of the sides of the triangle by using the cicumcircle of the triangle of the orthocenter together with that side.