Investigation of
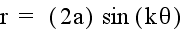
To start this investigation, again, we will look at the
graph of the above equation when a = 1 and k = 1.
 In this graph we see that equation is symmetric around
the y-axis and that it appears that the circle has a center of
1 on the polar scale.
To investigate further we will see what happens to
the graph when we vary the value of a...therefore let's explore
the graph of the equation when a = 3 and k = 1.
In this graph we see that equation is symmetric around
the y-axis and that it appears that the circle has a center of
1 on the polar scale.
To investigate further we will see what happens to
the graph when we vary the value of a...therefore let's explore
the graph of the equation when a = 3 and k = 1.
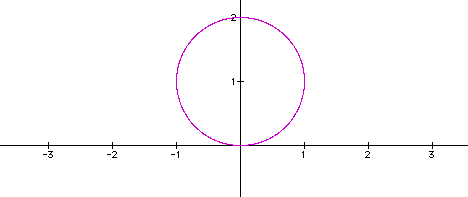
 It appears that the circle has expanded ...it now appears
that the center is equal to 3 on the polar scale.
Now let's see what happens when we vary the value of
k...so let's look at what happens if a = 1 and k = 2
It appears that the circle has expanded ...it now appears
that the center is equal to 3 on the polar scale.
Now let's see what happens when we vary the value of
k...so let's look at what happens if a = 1 and k = 2
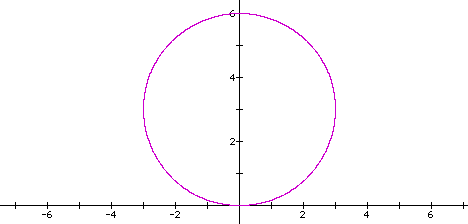
 It seems that if we allow k > 1 we get a completely
different type of graph...instead of a circle we have let's say
pedals.
Since the graph has 4 pedals...we could possible
assume that k times 2 would equal the number of pedals.
It seems that if we allow k > 1 we get a completely
different type of graph...instead of a circle we have let's say
pedals.
Since the graph has 4 pedals...we could possible
assume that k times 2 would equal the number of pedals.
Let's look at another graph to check...how about when k = 5 and
a is still equal to 1.
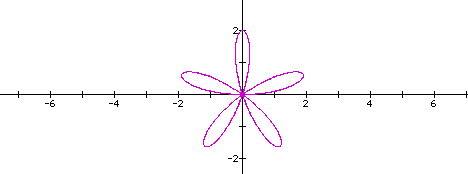 Here it looks like the number of pedals equals the
value of k
Click on the links to see the graphs when k
= 4 and k = 7.
After looking at these graphs we can assume that when
k is an even number, the number of pedals will be twice the value
of k. However, when k is an odd number, the number of pedals
is equal to the value of k.
Here it looks like the number of pedals equals the
value of k
Click on the links to see the graphs when k
= 4 and k = 7.
After looking at these graphs we can assume that when
k is an even number, the number of pedals will be twice the value
of k. However, when k is an odd number, the number of pedals
is equal to the value of k.
Now what happens when we vary both the values of "a"
and "k"?
Lets look when a = 3 and k = 5...if our assumptions
stand true we should get a graph with 5 pedals and the center
of the pedal being equal to 3.
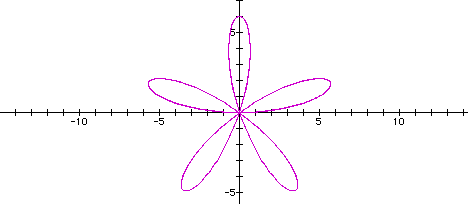 Yep, what do you know...we have a graph where the center
appears to be 3 and it does indeed have 5 pedals.
Yep, what do you know...we have a graph where the center
appears to be 3 and it does indeed have 5 pedals.
Return to Assign 11




