|
|
|
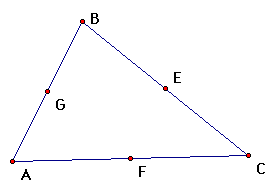
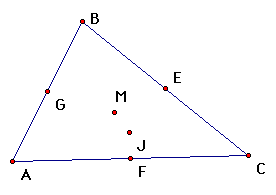
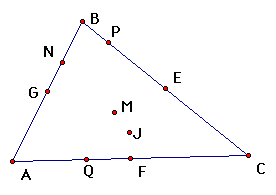
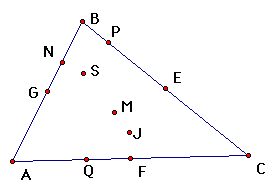
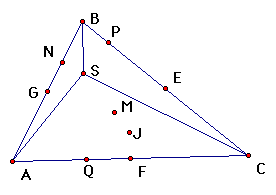
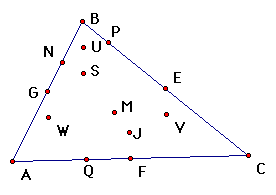
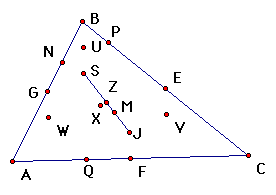
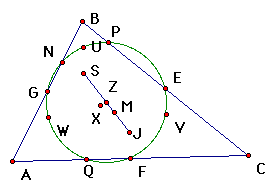
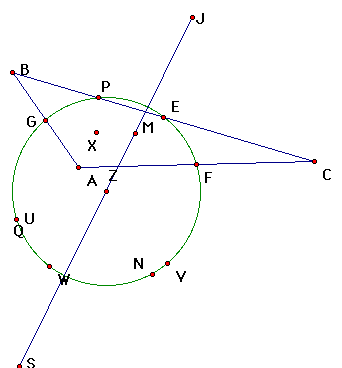
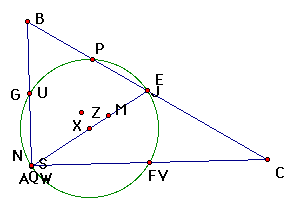
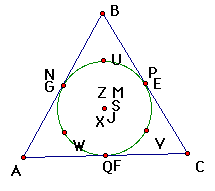
| midpoints of the three sides (3) |
|
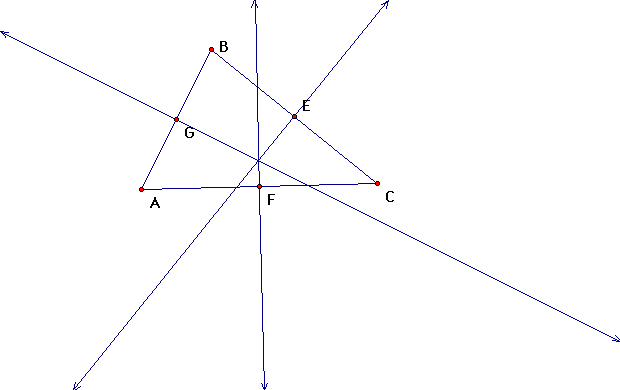
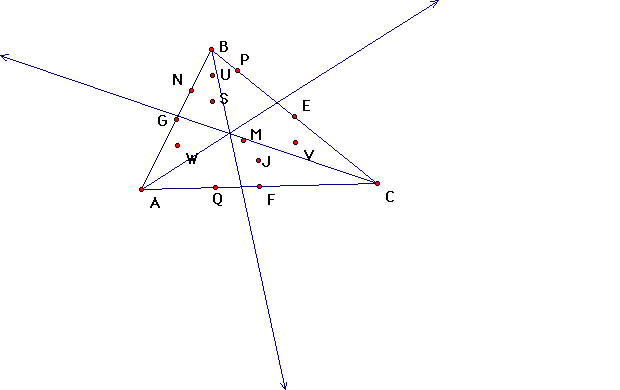
| circumcenter (1) |
|
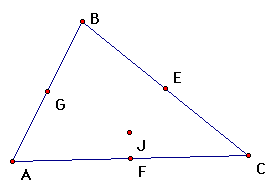
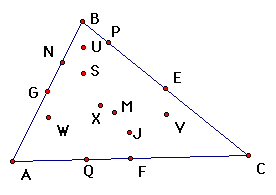
| centroid (1) |
|
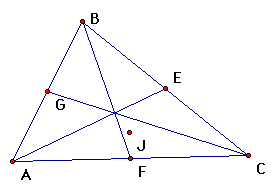
| intersection points of altitudes (3) |
|
| orthocenter (1) |
|
| midpoints of segments from orthocenter to each vertex (3) |
|
| incenter (1) |
|
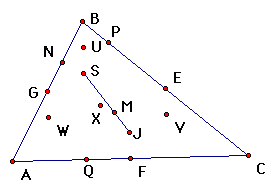
| midpoint of segment joining circumcenter and orthocenter |
|