Day 8 The Pythagorean Theorem
Objectives:
1) Use of the Pythagorean Theorem
2) Use of the converse of the Pythagorean Theorem
1) Draw a right triangle represented with geometric squares
as follows:
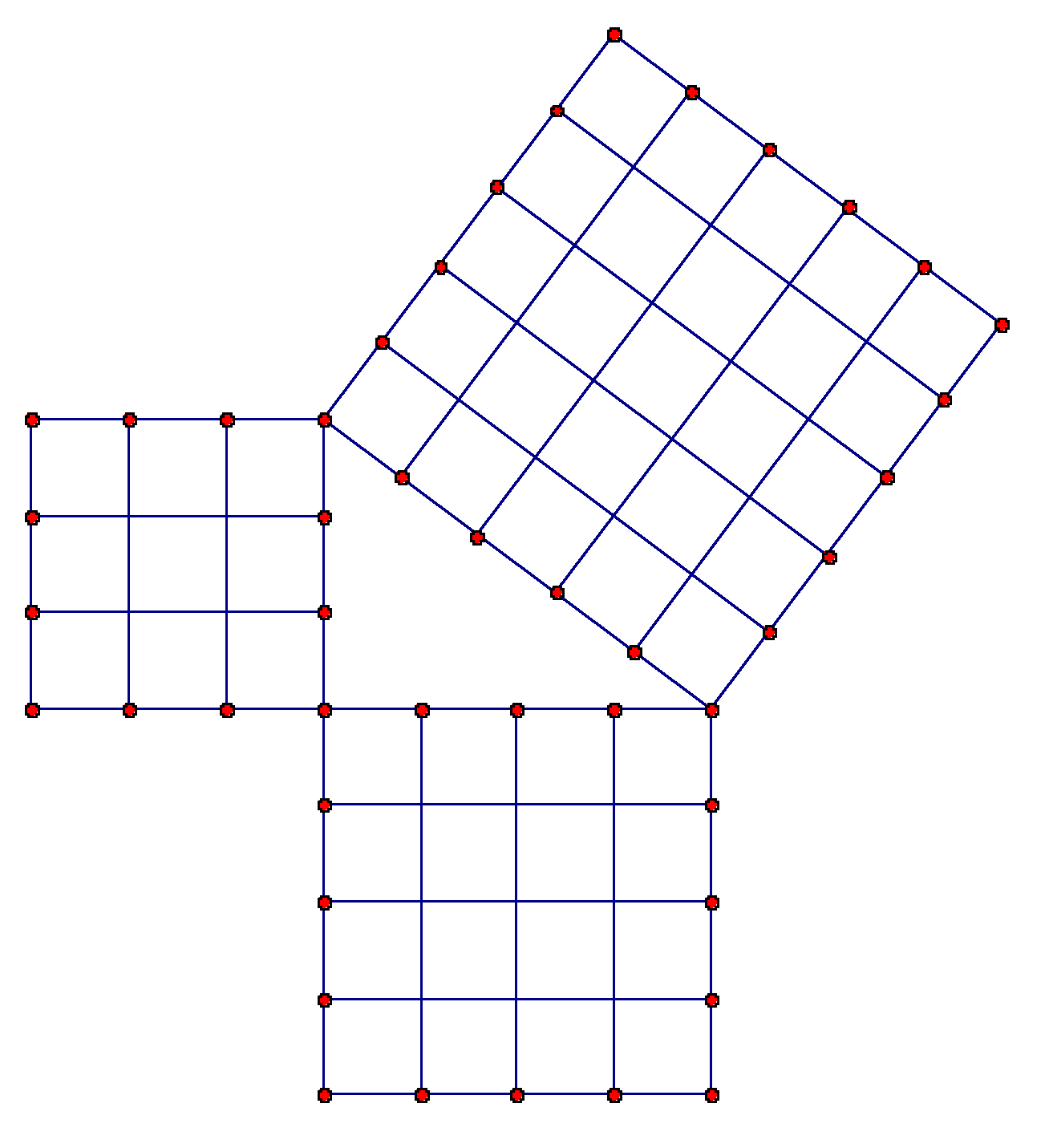
The sides of the right triangle have lengths 3, 4, and 5 units.
The area of the larger square is equal to the total area of the
two smaller squares.
This relationship is true for any right triangle
Have the students explore this concept with various size triangles
to show this is true.
2) State the Pythagorean Theorem
Pythagorean Theorem: In a right triangle, the square of the
length of the hypotenuse c is equal to the sum of the squares
of the lengths of the legs a and b.
Symbols: 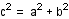
Practice Problem: Find the length of
the hypotenuse of several right triangles.
3) Explain to the students the converse of the Pythagorean
Theorem
Converse of the Pythagorean Theorem: If c is the measure
of the longest side of a triangle, a and b are the
lengths of the other two sides, and 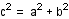 ,
then the triangle is a right triangle.
,
then the triangle is a right triangle.
Have the students determine whether certain triangles are
right triangles using the converse of the Pythagorean Theorem.
Practice Problem: The lengths of the
three sides of a triangle are 5, 7, and 9 inches. Determine whether
this triangle is a right triangle.

