Day 9 Pythagorean Triples
Objectives:
1) Definition of Pythagorean Triple
2) Definition of Primitive Pythagorean Triples
3) Finding Pythagorean Triples
1) Definition of Pythagorean Triple
Triple of positive integers (x,y,z)
in the case that it satisfies
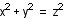
2) Definition of Primitive Pythagorean Triple
The triple is said to be primitive in
the case that no integer greater than 1 divides all of x,
y, and z
Of course, by the Pythagorean Theorem in any right triangle
whose sides have integral lengths, these lengths form a Pythagorean
Triple; and by its converse any such triple corresponds to a right
triangle.
The best known Pythagorean Triple is (3, 4, 5), which is primitive.
Other (nonprimitive) triples such as (6, 8, 10), (9, 12, 15)
and (30, 40, 50) can easily be formed from this one.
3) Finding Pythagorean Triples
Nonprimitive
It is easy to see that if (x, y, z)
is a Pythagorean Triple then so is (kx, ky, kz)
for any positive integer k.
We can see that any primitive Pythagorean Triple (x,
y, z) generates infinitely many nonprimitive ones
(kx, ky, kz), k = 2, 3, . Conversely,
any Pythagorean triple (x, y, z) corresponds
to a unique primitive one found by dividing x, y,
and z by their greatest common divisor.
Primitive
Pythagorean Triple Theorem:
Suppose that (x, y, z) is a primitive
Pythagorean triple with x even. Then there exists positive
integers u and v, whose greatest common divisor
is one, and not both odd, with u > v, such that
x = 2uv, 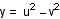 , and
, and
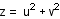
Conversely, if u and v are any pair of integers
as described in the previous sentence, and if x, y,
and z are defined by these three equations, then (x,
y, z) is a primitive Pythagorean triple with x
even.
Example:
The following table gives Pythagorean Triples corresponding
to some small values of u and v
u v x y z
2 1 4 3 5
3 2 12 5 13
4 1 8 15 17
4 3 24 7 25
Note: Any pair of positive integers u and v
with u > v will generate a Pythagorean Triple
(x, y, z) from the equations; the extra conditions
on u and v are necessary to guarantee that the triple is primitive
4) Have the students experiment on their own with the concepts
of Pythagorean Triples