The Broken Chord

Theorem of the Broken Chord

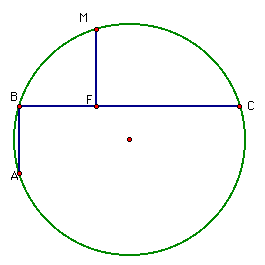
Given the figure below, the theorem states, "if AB and BC make up a broken chord in a circle, where BC > AB, and if M is the midpoint of arc ABC, then the foot F of the perpendicular from M on BC is the midpoint of the broken chord ABC.

Use GSP to find the measure of AB, BF and FC. Notice that the sumof AB and BC is equal to FC. Thereore, F is the midpoint of the broken chord.

Now use properties you have learned in this chapter to develop a proof as to why this is true. You may be working with isosceles, right and congruent triangles. Work in a small group and use the GSP sketch as guidance. Replicate this sketch and try different things.

HINT

SOLUTION

RETURN