

For our second fallacious proof, there is:
Consider circle O with point P inside the circle. Choose point R on ray OP so that (OP)(OR) = r squared (r^2), where r is the length of the radius of circle O. Let the perpendicular bisector of PR intersect circle O at points S and T; let M be the midpoint of PR.
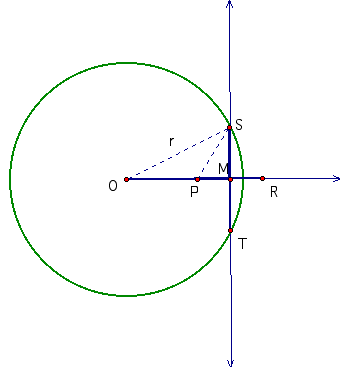
By multiplying (I) and (II):
By the Pythagorean theorem:
Now substitute (IV) and (V) into (III) to get:
Because segment OS is the radius of circle O:
Now substitute (VII) into (VI):
Therefore PS = 0, which implies that point P must be on the circle!
To discover the fallacy in this 'proof', we let OP = a. Therrefore OR = r^2/a. Because r > a and the square of a real number is positive, (r - a)^2 > 0. This can be written as r^2 - 2ra + a^2 > 2ra. Multiplying both sides of this inequality by 1/2a, we get 1/2(r^2/a + a) > r, which is /2 (OR + OP) > r, or OM > r. This imples that point M must be OUTSIDE the circle and that points S and T do not exist. This destroys the fallacious proof.
When this author tried to construct the circle according to the instructions, it was found to be impossible.