Assignment 3 Graphing Calculator: Quadratic EquationsCVKolodzy

Assignment # 12

Fall 2002 Semester

Spreadsheets - The Spreadsheet in Math Exploration

The Spreadsheet in Mathematics Explorations

Two different applications of the spreadsheet are shown in this example.

In the “Maximization of a Lidless Box”, the spreadsheet tool is used to iterate the problem to determine a solution.

In the “Cooling of Boiling Water” the different tools within the spreadsheet tools are used to determine an equation that approximates measured data.

Both tools are useful from the classroom perspective as methods to understand the mathematics behind the problem.

Some additional spreadsheet examples are provided at the end. See Other Examples...

Return to previous page...

Maximization of a Lidless Box

This example shows the effectiveness of the spreadsheet in the determination of a solution for a problem concerning maximization or minimization. The problem noted is one where the maximum volume of a lidless box is desired. A square, with square corners removed is given with an overall outside dimension of 5 X 8. How large should the square corners be? It is easily seen that the corners determine the height of the box desired. The height will impact the length and width (and subsequent volume)

The corners are cutout and folded along the lines shown.

The spreadsheet allows us to make multiple calculations of the volume of the open box, by changing the dimensions on the cutout squares in the corners.

Using S to represent the side dimension of the cutout squares, the relationship of S to the length, width and height of the box is as follows:

(Height) H = S

(Width) W = 5 – (2*S) ; The width is reduced by the twice the cutout side dimension.

(Length) L = 8 – (2*S) ; The length is also reduced by twice the cutout side dimension.

Volume = Height * Width * Lengt

V = S * (5 – (2*S)) * (8-(2*S))

V = S (5-2S)(8-2S)

V = 4S³ - 26S²+ 40S

Using the spreadsheet, we can setup a table where we start with values for S and progressively determine the height, length and width.

The table below shows the first pass, at determining the answer to the maximization problem:

Problems of Maximization
Lidless box formed by 5 X 8 sheet with a square removed from each corner….
x	8	5
Height	Length	Width	Volume
0.10	7.80	4.80	3.74
0.20	7.60	4.60	6.99
0.30	7.40	4.40	9.77
0.40	7.20	4.20	12.10
0.50	7.00	4.00	14.00
0.60	6.80	3.80	15.50
0.70	6.60	3.60	16.63
0.80	6.40	3.40	17.41
0.90	6.20	3.20	17.86
1.00	6.00	3.00	18.00
1.10	5.80	2.80	17.86
1.20	5.60	2.60	17.47
1.30	5.40	2.40	16.85
1.40	5.20	2.20	16.02
1.50	5.00	2.00	15.00
1.60	4.80	1.80	13.82
1.70	4.60	1.60	12.51
1.80	4.40	1.40	11.09
1.90	4.20	1.20	9.58
2.00	4.00	1.00	8.00
2.10	3.80	0.80	6.38
2.20	3.60	0.60	4.75
2.30	3.40	0.40	3.13
2.40	3.20	0.20	1.54
2.50	3.00	0.00	0.00

The highlighted area indicates an appropriate area to look further into the solution. The next two tables further expands the area of interest.

Height	Length	Width	Volume	Height	Length	Width	Volume
0.90	6.20	3.20	17.856	0.990	6.020	3.020	17.9986
0.91	6.18	3.18	17.884	0.991	6.018	3.018	17.9989
0.92	6.16	3.16	17.908	0.992	6.016	3.016	17.9991
0.93	6.14	3.14	17.930	0.993	6.014	3.014	17.9993
0.94	6.12	3.12	17.949	0.994	6.012	3.012	17.9995
0.95	6.10	3.10	17.965	0.995	6.010	3.010	17.9996
0.96	6.08	3.08	17.977	0.996	6.008	3.008	17.9998
0.97	6.06	3.06	17.987	0.997	6.006	3.006	17.9999
0.98	6.04	3.04	17.994	0.998	6.004	3.004	17.9999
0.99	6.02	3.02	17.999	0.999	6.002	3.002	18.0000
1.00	6.00	3.00	18.000	1.000	6.000	3.000	18.0000
1.01	5.98	2.98	17.999	1.001	5.998	2.998	18.0000
1.02	5.96	2.96	17.994	1.002	5.996	2.996	17.9999
1.03	5.94	2.94	17.988	1.003	5.994	2.994	17.9999
1.04	5.92	2.92	17.978	1.004	5.992	2.992	17.9998
1.05	5.90	2.90	17.966	1.005	5.990	2.990	17.9997
1.06	5.88	2.88	17.950	1.006	5.988	2.988	17.9995
1.07	5.86	2.86	17.933	1.007	5.986	2.986	17.9993
1.08	5.84	2.84	17.912	1.008	5.984	2.984	17.9991
1.09	5.82	2.82	17.890	1.009	5.982	2.982	17.9989
1.10	5.80	2.80	17.864	1.010	5.980	2.980	17.9986

The solution appears center around 1.000 for the maximum volume of the box. The solution can also be shown by performing the integration of the volume equation given the starting values. This in turn links the observed multiple calculations with the calculated values.

A copy of the spreadsheet used for this example is provided at the following link. (Note: EXCEL Spreadsheet - Office 2000 Version)

Lidless Box Spreadsheet

RETURN to TOP of PAGE

Cooling of Boiling Water – A Measurement Problem

The table of the measured temperature readings is provided below:

Minute	Temperature
0	212
1	205
2	201
3	193
4	189
5	184
6	181
7	178
8	172
9	170
10	167
11	163
12	161
13	159
14	155
15	153
16	152
17	150
18	149
19	147
20	145
21	143
22	141
23	140
24	139
25	137
26	135
27	133
28	132
29	131
30	130

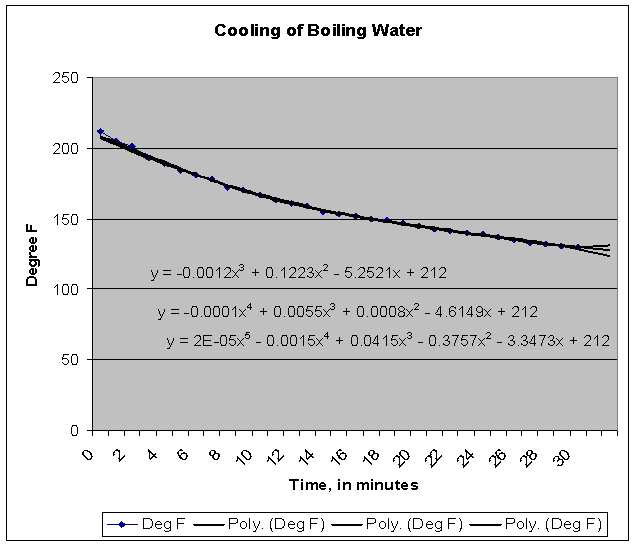
The graph of this table is provided below:

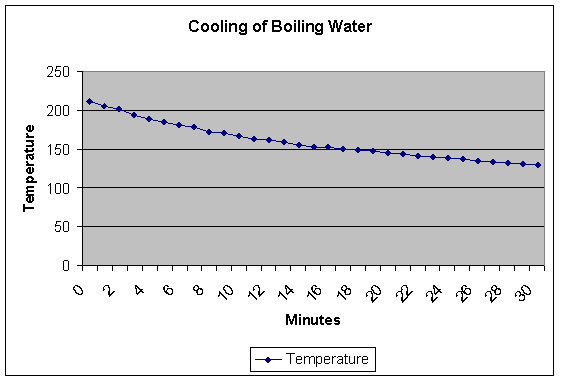
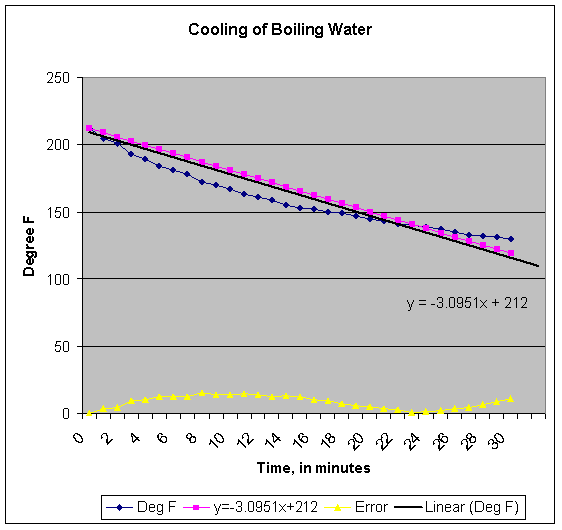
The graph shows an almost linear function. The spreadsheet function provides us with tools that will give us an approximate equation for the line. Using this tool, and forcing the y-intercept to be at 212 degrees F, yielded the following equation:

y = -3.0951x + 212

Minutes	Deg F	y=-3.0951x+212	Error
0	212	212	0
1	205	209	4
2	201	206	5
3	193	203	10
4	189	200	11
5	184	197	13
6	181	193	12
7	178	190	12
8	172	187	15
9	170	184	14
10	167	181	14
11	163	178	15
12	161	175	14
13	159	172	13
14	155	169	14
15	153	166	13
16	152	162	10
17	150	159	9
18	149	156	7
19	147	153	6
20	145	150	5
21	143	147	4
22	141	144	3
23	140	141	1
24	139	138	1
25	137	135	2
26	135	132	3
27	133	128	5
28	132	125	7
29	131	122	9
30	130	119	11

Substituting in the linear expression into the spreadsheet yields the table shown above. The plot of this is shown below. Can we do better at determining a calculation that will represent the observed data?

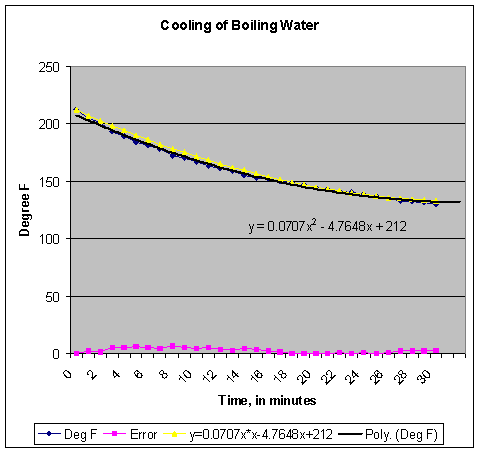
The tool allows us to try other types of equations to represent our data. A better approximation can be derived from choosing the polynomial solution method from the plotting function. As can be seen the 2^nd degree polynomial chosen yield the following:

y = 0.0707x – 4.7648x + 212

Minutes	Deg F	y=0.0707x*x-4.7648x+212	Error
0	212	212	0
1	205	207	2
2	201	203	2
3	193	198	5
4	189	194	5
5	184	190	6
6	181	186	5
7	178	182	4
8	172	178	6
9	170	175	5
10	167	171	4
11	163	168	5
12	161	165	4
13	159	162	3
14	155	159	4
15	153	156	3
16	152	154	2
17	150	151	1
18	149	149	0
19	147	147	0
20	145	145	0
21	143	143	0
22	141	141	0
23	140	140	0
24	139	138	1
25	137	137	0
26	135	136	1
27	133	135	2
28	132	134	2
29	131	133	2
30	130	133	3

The graph of the plot follows. This is a much better approximation of the observed data.

By further expanding the polynomial(3^rd, 4^th and 5^th degree), it can be seen that we do not seem to get much closer to the measurement data. Some examples with the data are shown below:

3^rd Degree Polynomial Solution:

y = -0.0012x³ + 0.1223x² - 5.2521x + 212

4^th Degree Polynomial Solution:

y = -0.0001x⁴ + 0.0055x³ + 0.0008x² – 4.6149x + 212

5^th Degree Polynomial Solution:

y = 2E-05x⁵ – 0.0015x⁴+ 0.0415x³ – 0.3757x² – 3.3473x + 212

Minutes	Deg F	3rd Degree Polynomial	Error	4th Degree Polynomial	Error	5th Degree Polynomial	Error
0	212	212	0	212	0	212	0
1	205	207	2	207	2	208	3
2	201	202	1	203	2	204	3
3	193	197	4	198	5	200	7
4	189	193	4	194	5	195	6
5	184	189	5	190	6	190	6
6	181	185	4	185	4	186	5
7	178	181	3	181	3	181	3
8	172	177	5	178	6	177	5
9	170	174	4	174	4	173	3
10	167	171	4	170	3	169	2
11	163	167	4	167	4	166	3
12	161	165	4	164	3	163	2
13	159	162	3	161	2	161	2
14	155	159	4	159	4	159	4
15	153	157	4	156	3	157	4
16	152	154	2	154	2	155	3
17	150	152	2	152	2	154	4
18	149	150	1	151	2	152	3
19	147	148	1	149	2	151	4
20	145	146	1	148	3	151	6
21	143	145	2	147	4	150	7
22	141	143	2	146	5	150	9
23	140	141	1	145	5	150	10
24	139	140	1	145	6	151	12
25	137	138	1	144	7	151	14
26	135	137	2	144	9	153	18
27	133	136	3	143	10	154	21
28	132	134	2	143	11	157	25
29	131	133	2	142	11	160	29
30	130	132	2	142	12	165	35

The graphs of the 3^rd, 4^th and 5^th degree polynomials shows the “spreading” of the lines representing the equations as we approach the end point of 30 minutes.

Investigations of power, exponential and logarithmic functions do not give us any better results than the 2^nd degree polynomial fit. The best fit equation for each is as follows:

Power Function: y = 237.82x^-0.1624

Logarithmic Function: y = -27.097Ln(x) + 227.84

Exponential Function: y = 212e^-0.0177x

We can also split the graph into two linear or 2^nd degree polynomial equations. The results of this are shown in the attached table. As can be seen, 2 linear expressions can approximate better than the single linear expression, but still not as good as the 2^nd degree polynomial.

Minutes	Deg F	Linear	Error	2nd Degree Poly	Error
0	212	212	0	212	0
1	205	208	3	207	2
2	201	204	3	203	2
3	193	200	7	198	5
4	189	196	7	194	5
5	184	192	8	189	5
6	181	188	7	185	4
7	178	184	6	181	3
8	172	180	8	178	6
9	170	176	6	174	4
10	167	172	5	170	3
11	163	167	4	167	4
12	161	163	2	164	3
13	159	159	0	161	2
14	155	155	0	158	3
15	153	151	2	155	2
16	152	147	5	152	0
			65		51

Minutes	Deg F	Linear	Error	2nd Degree Poly	Error
15	153	153	0	153	0
16	152	152	0	152	0
17	150	150	0	150	0
18	149	149	0	149	0
19	147	147	0	148	1
20	145	146	1	146	1
21	143	144	1	145	2
22	141	143	2	143	2
23	140	141	1	142	2
24	139	140	1	140	1
25	137	138	1	139	2
26	135	137	2	137	2
27	133	136	3	136	3
28	132	134	2	134	2
29	131	133	2	132	1
30	130	131	1	131	1
			18		21
			83		72

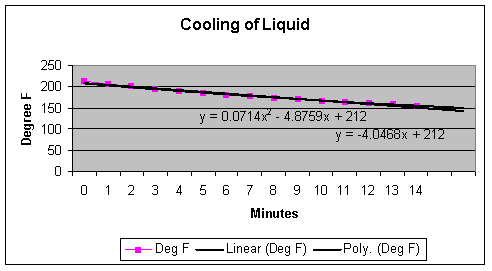
The first of the two graphs below reflect the appropriate equations for the first half of the recorded points. The equations determined by the spreadsheet were:

Linear: y = -4.0468x + 212

2^nd degree Polynomial: y = 0.0714x² – 4.8759x + 212

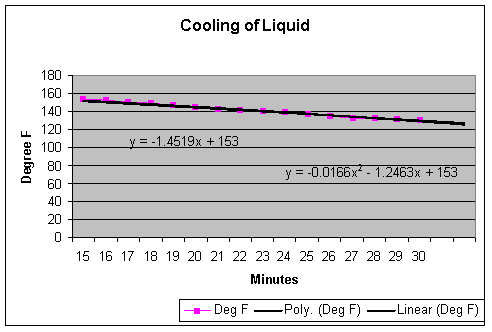
The second graph reflect the equations for the 2^nd half of the points. Please note that the equations given by the spreadsheet tool reflect the time element effectively beginning at 0 rather than at 15. The equations effectively are:

Linear: y = -1.4519(x-15) + 153

2^nd degree Polynomial: y = -0.0166(x-15)² -1.2463(x-15) + 153

Some additional questions may be asked – such as predicting when the liquid would cool to a specified temperature – e.g. 100 def F or room temperature (75 deg F).

Each of the equations derived from the plots can be investigated with various results. We can either perform the calculation directly from the equation, or extend the tables within the spreadsheet. The single equation solutions, both linear and 2^nd degree polynomial yield less than desirable results:

	Single Equation		Dual Equation
Minutes	Linear	2nd Degree Poly	Linear	2nd Degree Poly
31	116	132	130	129
32	113	132	128	127
33	110	132	127	125
34	107	132	125	123
35	104	132	124	121
36	101	132	123	120
37	97	132	121	118
38	94	133	120	116
39	91	134	118	114
40	88	135	117	111
41	85	135	115	109
42	82	137	114	107
43	79	138	112	105
44	76	139	111	103
45	73	141	109	101
46	70	142	108	98
47	67	144	107	96
48	63	146	105	94
49	60	148	104	91
50	57	151	102	89
51	54	153	101	87
52	51	155	99	84
53	48	158	98	82
54	45	161	96	79
55	42	164	95	77
56	39	167	93	74
57	36	170	92	71
58	32	173	91	69
59	29	177	89	66
60	26	181	88	63

A graphic representation follows:

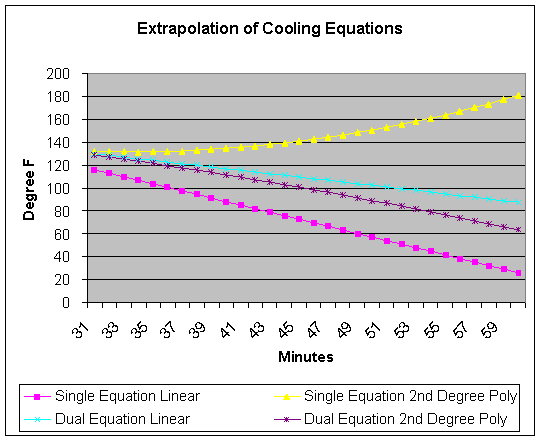
For the linear equation we see that we reach 100 deg F in about 37 minutes and 75 deg F in about 45 minutes. This is not too surprising; however, the equation yields temperatures below room temperature (actually below freezing) within an hour. This equation appears not to be a very good predictor. It is important that this type of result be explained when presenting to classes. Curve fitting techniques are typically focused on discrete ranges. When the ranges investigated exceed the range initially defined, then poor results are possible.

This is further seen with the 2^nd degree polynomial expression. There are no valid solutions for y = 100 or y = 75. When we examine this with the spreadsheet, it is evident that the temperature values extrapolated for later times, the temperature values begin to rise. Again, this points out the dangers in extrapolation of what appeared to be a valid representation of the data between 0 and 30 minutes.

When we split the equations for the first 15 minutes and the last 15 minutes, then we have better results on the determination of time for 100 deg F and 75 deg F. As can be seen, the results seem more realistic. In the points of discussing this with a class, here it can be noted that the other parameters that affect the change in temperature over time may be necessary to better approximate the expected temperature over time. E.g ambient temperature, thermal properties of the container.

A copy of the spreadsheet used for this example is provided at the following link. (Note: EXCEL Spreadsheet - Office 2000 Version)

Cooling Water Spreadsheet

RETURN to TOP of PAGE

Other Examples:

Some additional spreadsheet examples are provided below:

Factorial Example

Sine / Cosine Example

Fibonacci Example

Savings/Credit Card Example

Absolute Differences - 4 Numbers

Return to Previous Page